Критерий качества организации системыНапомним, что в первой части мы рассмотрели основные особенности самоорганизующихся систем.Интуитивно, отсутствие организации отождествляется с хаосом. На основании этой интуитивной предпосылки, в кибернетике появилось специфическое понятие организации, которое применимо к широкому кругу объектов и систем и дает численную меру статистических связей между элементами системы - R.
Это понятие основано на следующих рассуждениях. Пусть имеется некая система, которая состоит из отдельных частей или подсистем (не обязательно однородных). Каждая из этих подсистем, в процессе их существования или деятельности может принимать некоторое множество состояний, над которым задано конкретное распределение вероятностей.
Если все подсистемы разобщены, то есть поведение одной подсистемы никак не влияет на поведение других, или, иными словами, все подсистемы независимы, то система будет являться предельно неорганизованной.
Другой предельный (идеальный) случай – когда состояние одной подсистемы однозначно определяет состояние всех остальных.
Если подсистемы разобщены, то энтропия множества состояний каждой подсистемы Zможет быть определена следующим образом:
H(Z) = - 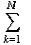 Pk log2 Pk Pk log2 Pk | (2.1) |
|
|
где k= 1, 2, … N– возможные состояния подсистемы Zi, а Pik– вероятность того, что эта подсистема окажется в состоянии k. При этом если Pk=0.5, то
В предельно неорганизованной системе общая энтропия будет максимальна и равна сумме энтропий её подсистем. Так, для системы, состоящей из двух подсистем – Z*и Z**, будем иметь:
H0 (Z*, Z**) = H (Z*) + H (Z**) | (2.3) |
|
|
Если в системе имеются связи между её элементами (подсистемами), то есть эти элементы взаимно влияют друг на друга, то система организуется, и общая энтропия становится меньше суммы энтропий её элементов, и будет составлять:
H1 (Z*, Z**) = H (Z**) + H (Z*|Z**) = H (Z*) + H (Z**|Z*) | (2.4) |
|
|
где H(Z*|Z**) – условная энтропия, которая определяется выражением:
H (Z*|Z**) = - 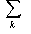 P(Zk**) P(Zk**) 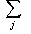 P(Zj *|Zk**) log2 P(Zj *|Zk**) P(Zj *|Zk**) log2 P(Zj *|Zk**) | (2.5) |
где P(Zj*|Zk**) – вероятность состояния Zj*, если имеет место состояние Zk**.
Величина H(Z*|Z**) всегда удовлетворяет следующему условию:
0 H (Z*|Z**) H (Z*) | (2.6) |
|
|
при этом величина H(Z*|Z**)=0 только в том случае, если каждое состояние Zj* однозначно определяется состоянием Zk**. При таких условиях все P(Zj*|Zk**)=1, и H(Z*|Z**)=0 (в силу того, что log1=0). Данный случай соответствуют идеальной организации системы.
Таким образом, в результате организации системы её энтропия H1будет ниже максимальной энтропии H0. Это уменьшение энтропии может служить численной мерой организованности системы – R:
R = H0 – H1 = H (Z*) - H(Z*|Z**) | (2.7)
|
при этом величина R=0 будет соответствовать предельно неорганизованной системе, а величина R=Н(Z*) – системе, которая организована идеально.
Следует отметить, что величина Rопределяет уровень организации системы в процессе её функционирования (в динамике), а именно: величина Rможет быть больше нуля только тогда, когда система способна адаптироваться к изменениям состояний её элементов.

