Очевидно, что при изучении и имитации процессов движения пакетов по сети, необходимо учитывать, по крайней мере, следующие факторы:

1) распределение радиочастот;

2) изменчивые условия радиослышимости;

3) и, наконец, распределение потоков информации, которое может изменяться при адаптации системы к возникшим ситуациям.

Совокупность радиочастот и потенциальная возможность их использования теми или иными станциями может быть описана гиперграфом H=(Е,W), вершины которого соответствуют узлам сети, а подмножества w_k W- используемым частотам. Описание гиперграфа H=(E,W) может быть задано либо в форме списков w_k={Xi₁, Xi₂, . . . , Xi_N}, либо в виде матрицы инциденций ║S_ik║ элемент которой

Например, изображённый на рисунке 1 гиперграф может быть представлен в виде матрицы ║S_ik║, представленной на рисунке 2:

Рисунок 1

Рисунок 2

Элементы X_iw_1w₂ соответствуют узлам, которые могут воспользоваться как частотойw₁, так и частотойw₂. 

Условия радиослышимости могут быть описаны неориентированным графом G=(E,Г), вершины которого соответствуют узлам сети. Вершины, которые соответствуют парам слышащих друг друга абонентов, соединяются ребром.

Следует подчеркнуть, что в такой граф включаются далеко не все потенциально возможные соединения. Например, изображенному на рисунке 1 гиперграфу может соответствовать граф, изображённый на рисунке 3: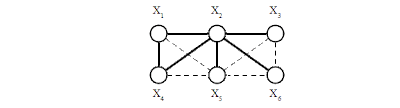

Рисунок 3

Граф G=(E,Г) может быть описан матрицей смежности - A=║A_ij║. Число строк и столбцов такой матрицы должно соответствовать числу узлов в сети. Элементы матрицы ║A_ij║ отражают структуру графа G=(E,Г), соответствующего текущему состоянию сети:

Например, изображённому на рисунке 3 графу будет соответствовать матрица, показанная на рисунке 4:

Рисунок 4

Содержимое матрицы A_ij периодически изменяется, что имитирует процесс изменений условий радиослышимости.

Эти вероятности могут быть заданы в виде матрицы P=║P_ij║, каждый элемент которой, соответствует потенциально возможному радиолучу, заданному гиперграфом H=(Е,W), а значение этого элемента – вероятности существования этого радиолуча.

При наличии такой матрицы, генерация ситуаций, связанных с отказами/восстановлениями радиолучей может осуществляться с помощью следующего алгоритма:

1) матрица A=║A_ij║ «обнуляется»;

2) поочерёдно просматриваются элементы матрицы P, отвечающие условию (1):

3) если просматриваемый элемент отвечает условию (2)

то

- генерируется случайное число - x, в интервале {0, …, 1};

- проверяется условие (3):

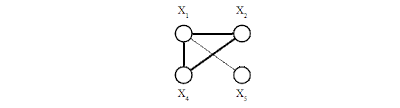
и, если условие (3) выполняется, то в граф G=(E,Г) добавляется две дуги - (X_i,X_j) и (X_j,X_i).

Отметим, что, при выборке ситуаций, изменения структуры сети не считаются необратимыми – генерация новых ситуаций всегда опирается на заданное описание сети – гиперграф H=(Е,W).

Приведённый алгоритм может быть проиллюстрирован следующим примером. Рассмотрим заданный пользователем фрагмент сети, который представлен на рисунке 5:

Рисунок 5

Допустим, что станции X₁, X₂ и X₄ не меняют своей дислокации и связь между ними устойчива, а станция X₅ может потерять связь с любой из этих станций, поскольку место её дислокации выбрано неудачно.

Этому фрагменту может быть поставлена в соответствие матрица P, которая представлена на рисунке 6.

Рисунок 6

Предположим теперь, что при выполнении приведённого алгоритма, датчик случайных чисел сформировал следующие значения x:

При таких значениях x матрица A=║A_ij║ будет иметь вид, представленный на рисунке 7, а соответствующий граф G=(E,Г) будет иметь вид, представленный на рисунке 8:

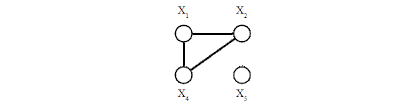
Рисунок 7

Рисунок 8

(Обратим внимание на то, что при рассмотрении величин P_ij=1 и P_ij=0, случайные числа x не играют никакой роли – если P_ij=1, то в граф G=(E,Г) всегда будет включено соответствующее ребро, и наоборот - если P_ij=0, то вершины X_iи X_jне будут считаться смежными).

Очевидно, что при использовании рассматриваемого алгоритма (при иных значениях x), может быть построены четыре варианта графа G=(E,Г) - на рисунке 8 приведён только один из них. Но возможны ещё три варианта:

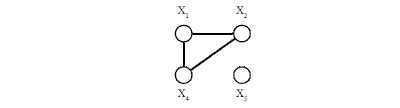
Рисунок 9

Рисунок 10

Рисунок 11

2.3. Таким образом, в результате имитации процессов отказов/восстановлений радиолучей, мы можем получить любые структуры, и, имея граф G=(E,Г) - установить возможность успешной доставки пакетов по всем заданным маршрутам. Для этого необходимо иметь план распределения нагрузки в сети, который определён процедурами маршрутизации.

Этот план может быть представлен в виде множества суграфов G_a=(E,Г_a), каждый из которых соответствует конкретному узлу-получателю - .X_a.

Например, для представленного на рисунке 1 примера сети, суграф G₁=(E,Г₁) может иметь вид, представленный на рисунке 12:

Рисунок 12

Такой суграф может быть описан в виде матрицы смежности – M^(a) =║M_ij^(a)║, элемент которой

Например, представленный на рисунке 12 суграф может быть оформлен в виде матрицы, которая показана на рисунке 13: