|
Какой рейтинг вас больше интересует?
|
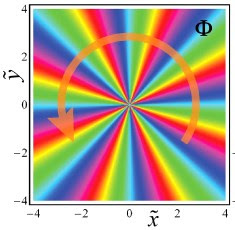
Вращение закрученной волны2013-07-29 21:02:00 (читать в оригинале)Я тут на днях написал две популярных заметки для «Элементов» про закрученный свет и закрученные электроны, и еще отдельно про закрученный рентген. Заметки вызвали некоторый интерес и разные вопросы. В комментах к моему старому посту в блоге про закрученные фотоны было сделано хорошее наблюдение: увеличение «силы закрутки» сопровождается замедлением вращения. Вывод, казалось бы, парадоксальный. Я подумал, что полезно будет вынести в отдельный пост объяснение, почему никакого парадокса тут нет. (Пост получился немножко технический, с формулами, но что ж поделать.) 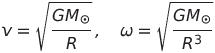  Теперь о том, что происходит с закрученной волной. Для простоты забудем про поляризацию, она на сущность «парадокса» не влияет. И еще будем рассматривать совсем простой вариант закрученной волны — так называемый бесселев пучок. Он представляет из себя суперпозицию плоских волн, приходящих под одинаковыми полярными углами, но под разными азимутальными углами к оси z, ну и с правильной настройкой относительных фаз. Бесселевы пучки хоть и менее физичны, чем лагерр-гауссовы пучки, которые обычно в этих задачах рассматриваются, но они проще для изучения и иллюстрации. Так вот, волновая функция бесселева пучка в поперечной плоскости (полярные координаты R и φ) имеет такой вид:
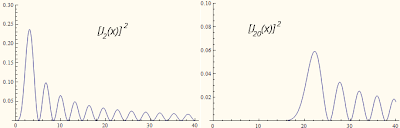
А теперь посмотрим на формулу внимательнее и заметим, что значение m влияет не только на угловую зависимость, но и на радиальную, ведь там стоит бесселева функция именно m-го порядка. Как выглядит график бесселевой функции для разных m? Для примера на рис. 2 нарисован квадрат функций J2(x) и J20(x).
Пользуясь механической аналогией, можно сказать, что с ростом m, у пучка словно увеличивается момент инерции (для чисто бесселевого пучка это некорректное заявление, но это уже мелочи). Да, при этом скорость вращения замедляется, но этот момент инерции с лихвой компенсирует это замедление. И в результате орбитальный угловой момент растет пропорционально m как раз за счет этой «перекомпенсации» (формулы для механической аналогии написать совсем несложно). Такая вот небольшая тонкость.
|
Категория «Блогосфера»
Взлеты Топ 5
Падения Топ 5
Популярные за сутки
|
Загрузка...
BlogRider.ru не имеет отношения к публикуемым в записях блогов материалам. Все записи
взяты из открытых общедоступных источников и являются собственностью их авторов.
взяты из открытых общедоступных источников и являются собственностью их авторов.