Какой рейтинг вас больше интересует?
|
Главная / Главные темы / Тэг «сергеевич»

Кузьма Сергеевич Петров-Водкин 2012-11-15 10:59:57
Кузьма Сергеевич Петров-Водкин родился ...
+ развернуть текст сохранённая копия
Кузьма Сергеевич Петров-Водкин родился 5 ноября 1878 года в Российской империи Саратовской губернии городе Хвалынске в семье сапожника. При поддержке местных купцов сумел получить художественное образование: в городе Самаре учился в классе рисования и живописи у Федора Емельяновича Бурова; в … Continue reading →
Тэги: классик, кузьма, петров-водкин, подборка, сергеевич
Михаил Сергеевич Евдокимов, заслуженный артист РФ, политический деятель. 2012-05-30 14:20:55
Михаил Сергеевич Евдокимов – артист ...
+ развернуть текст сохранённая копия
Михаил Сергеевич Евдокимов – артист эстрады, юморист, киноактёр, исполнитель песен, заслуженный артист РФ, глава администрации Алтайского края. Михаил Евдокимов родился 6 декабря 1957 года в городе Сталинске (Новокузнецк) Кемеровской области. Отец, Сергей Васильевич — рабочий. Мать, Анна Петровна работала на шахте. В 1958 году семья переехала в село Верх-Обское Смоленского района Алтайского края. По окончании [...]
Тэги: евдокимов, история, михаил, сергеевич
Есть еще одно занятие - Экзамен по эконометрике сдавать... 2011-10-30 21:54:54
... по ТРУСОВУ Александру Сергеевичу, не если и ...
+ развернуть текст сохранённая копия
Чтоб пусто было тому человеку кто в совершенстве знает эконометрику.... А если её ведет Трусов, то я уверен, что мало кто её знает впринципе =))) Этот пост чисто для меня, ибо сижу как дурак, готовлюсь к экзамену, к предмету которого не знаю... сколько раз я готовился и сдавал подобные сессии... но такой ещё не было. То что иде после черты не обязательно есть в вопросах по ТРУСОВУ Александру Сергеевичу, не если и этого не знать, или хотябы не прочесть то хана.
________________________________________________________________________________________________________________
________________________________________________________________________________________________________________
1 Эконометрика — наука, изучающая количественные и качественные экономические взаимосвязи с помощью математических и статистических методов и моделей[1]. Современное определение предмета эконометрики было выработано в уставе Эконометрического общества, которое главными целями назвало использование статистики и математики для развития экономической теории[2]. Теоретическая эконометрика рассматривает статистические свойства оценок и испытаний, в то время как прикладная эконометрика занимается применением эконометрических методов для оценки экономических теорий.
Эконометрический метод складывался в преодолении следующих неприятностей, искажающих результаты применения классических статистических методов:
• асимметричности связей;
• мультиколлинеарности объясняющих переменных;
• закрытости механизма связи между переменными в изолированной регрессии;
• эффекта гетероскедастичности, т. е. отсутствия нормального распределения остатков для регрессионной функции;
• автокорреляции;
• ложной корреляции;
• наличия лагов.
Эконометрическая модель, как правило, основана на теоретическом предположении о круге взаимосвязанных переменных и характере связи между ними. При всем стремлении к «наилучшему» описанию связей приоритет отдается качественному анализу. Поэтому в качестве этапов эконометрического исследования можно указать:
• постановку проблемы;
• получение данных, анализ их качества;
• спецификацию модели;
• оценку параметров;
• интерпретацию результатов.
3. Линейное уравнение регрессии, коэффициенты модели.
Линейная модель парной регрессии есть: у=а0+а1х+
а1 - коэф-т регрессии, показывающий, как изменится у при изменении х на единицу
а0 - это свободный член, расчетная величина, содержания нет.
- это остаточная компонента, т.е. случайная величина, независимая, нормально распределенная, мат ожид = 0 и постоянной дисперсией.
В матричной форме модель имеет вид:
Y=XA+ε
Где Y– вектор-столбец размерности (nx1) наблюдаемых значений зависимой переменной; Х– матрица размерности (nx2) наблюдаемых значений факторных признаков. Дополнительный фактор х0 вводится для вычисления свободного члена; А– вектор-столбец размерности (2х1) неизвестных, подлежащих оценке коэффициентов регрессии; ε– вектор-столбец размерности (nх1) ошибок наблюдений
;
Параметры модели находятся с использованием МНК. Подсчитывается сумма квадратов ошибок наблюдений.
4 ЛИНЕЙНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ: СМЫСЛ И ОЦЕНКА ПАРАМЕТРОВ
Линейная регрессия сводится к нахождению уравнения вида или .
Уравнение вида позволяет по заданным значениям фактора x иметь теоретические значения результативного признака, подставляя в него фактические значения фактора х.
Построение линейной регрессии сводится к оценке ее пара¬метров а и в.
Оценки параметров линейной регрессии могут быть найдены разными методами.
1.
2.
Параметр b называется коэффициентом регрессии. Его вели¬чина показывает среднее изменение результата с изменением фактора на одну единицу.
Формально а — значение у при х = 0. Если признак-фактор
не имеет и не может иметь нулевого значения, то вышеуказанная
трактовка свободного члена, а не имеет смысла. Параметр, а может
не иметь экономического содержания. Попытки экономически
интерпретировать параметр, а могут привести к абсурду, особенно при а < 0.
Интерпретировать можно лишь знак при параметре а. Если а > 0, то относительное изменение результата происходит медленнее, чем изменение фактора.
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции rxy. Существуют разные модификации формулы линейного коэф¬фициента корреляции.
Линейный коэффициент корреляции находится и границах: -1≤.rxy ≤ 1. При этом чем ближе r к 0 тем слабее корреляция и наоборот чем ближе r к 1 или -1, тем сильнее корреляция, т.е. зависимость х и у близка к линейной. Если r в точности =1или -1 все точки лежат на одной прямой. Если коэф. регрессии b>0 то 0 ≤.rxy ≤ 1 и наоборот при b<0 -1≤.rxy ≤0. Коэф. корреляции отражает степени линейной зависимости м/у величинами при наличии ярко выраженной зависимости др. вида.
Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции , называемый коэффициентом детерминации. Коэффициент детермина¬ции характеризует долю дисперсии результативного признака y, объясняемую регрессией. Соответствующая величина характеризует долю дисперсии у, вызванную влиянием остальных не учтенных в модели факторов.
5. ОЦЕНКА СУЩЕСТВЕННОСТИ ПАРАМЕТРОВ ЛИНЕЙНОЙ РЕГРЕССИИ И КОРРЕЛЯЦИИ.
Оценка значимости уравнения регрессии в целом дается с по¬мощью F-критерия Фишера. При этом выдвигается нулевая ги¬потеза, что коэффициент регрессии равен нулю, т. е. b = 0, и следовательно, фактор х не оказывает влияния на результат у.
Непосредственному расчету F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложе¬ние общей суммы квадратов отклонений переменной у от средне го значения у на две части - «объясненную» и «необъясненную»:
- общая сумма квадратов отклонений
- сумма квадратов отклонения объясненная регрессией - остаточная сумма квадратов отклонения.
Любая сумма квадратов отклонений связана с числом степе¬ней свободы, т. е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности nис числом определяемых по ней констант. Применительно к исследуемой проблеме число cтепеней свободы должно показать, сколько независимых откло¬нений из п возможных требуется для образования данной суммы квадратов.
Дисперсия на одну степень свободы D.
F-отношения (F-критерий):
Ecли нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для Н0 необходимо опровержение, чтобы факторная дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором раз¬работаны таблицы критических значений F-отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение F-критерия — это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признается достоверным, если о больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: Fфакт > Fтабл Н0 отклоняется.
Если же величина окажется меньше табличной Fфакт ‹, Fтабл , то вероятность нулевой гипотезы выше заданного уровня и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым. Но не отклоняется.
Стандартная ошибка коэффициента регрессии
Для оценки существенности коэффициента регрессии его ве¬личина сравнивается с его стандартной ошибкой, т. е. определяется фактическое значение t-критерия Стьюдентa: которое
затем сравнивается с табличным значением при определенном уровне значимости и числе степеней свободы (n- 2).
Стандартная ошибка параметра а:
Значимость линейного коэффициента корреляции проверя¬ется на основе величины ошибки коэффициента корреляции тr:
Общая дисперсия признака х:
Коэф. регрессии Его величина показывает ср. изменение результата с изменением фактора на 1 ед.
Ошибка аппроксимации:
6,5. ИНТЕРВАЛЫ ПРОГНОЗА ПО ЛИНЕЙНОМУ УРАВНЕНИЮ РЕГРЕССИИ
Оценка стат. значимости параметров регрессии проводится с помощью t – статистики Стьюдента и путем расчета доверительного интервала для каждого из показателей. Выдвигается гипотеза Н0 о статистически значимом отличие показателей от 0 a = b = r = 0. Рассчитываются стандартные ошибки параметров a,b, r и фактич. знач. t – критерия Стьюдента.
Определяется стат. значимость параметров.
ta ›Tтабл - a стат. значим
tb ›Tтабл - b стат. значим
Находятся границы доверительных интервалов.
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что параметры a и b находясь в указанных границах не принимают нулевых значений, т.е. не явл.. стат. незначимыми и существенно отличается от 0.
7. НЕЛИНЕЙНАЯ РЕГРЕССИЯ. ВИДЫ МОДЕЛЕЙ
Если между экономическими явлениями существуют нели¬нейные соотношения, то они выражаются с помощью соответ¬ствующих нелинейных функций: например, равносторонней ги¬перболы , параболы второй степени и д.р.
Различают два класса нелинейных регрессий:
• регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым па¬раметрам;
• регрессии, нелинейные по оцениваемым параметрам.
Примером нелинейной регрессии по включаемым в нее объ¬ясняющим переменным могут служить следующие функции:
• полиномы разных степеней
• равносторонняя гипербола
К нелинейным регрессиям по оцениваемым параметрам от¬носятся функции:
• степенная
• показательная
экспоненциальная
8,9 ПРИМЕНЕНИЕ МНК К МОДЕЛЯМ НЕЛИНЕЙНЫМ ОТНОСИТЕЛЬНО ВКЛЮЧАЕМЫХ ПЕРЕМЕННЫХ И ОЦЕНИВАЕМЫХ ПАРАМЕТРОВ.
Нелинейная регрессия по включенным переменным не таит каких-либо сложностей в оценке ее параметров. Она определяет¬ся, как и в линейной регрессии, методом наименьших квадратов (МНК), ибо эти функции линейны по параметрам. Так, в парабо¬ле второй степени y=a0+a1x+a2x2+ε заменяя переменные x=x1,x2=x2, получим двухфакторное урав¬нение линейной регрессии: у=а0+а1х1+а2х2+ ε
Парабола второй степени целесообразна к применению, если для определенного интервала значений фактора меняется харак¬тер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую. В этом случае определяется значение фактора, при котором достигается максимальное (или минимальное), значение результативного признака: приравнива¬ем к нулю первую производную параболы второй степени: , т.е. b+2cx=0 и x=-b/2c
Применение МНК для оценки параметров параболы второй степени приводит к следующей системе нормальных уравнений:
Решение ее возможно методом определителей:
В моделях, нелинейных по оцениваемым параметрам, но приводимых к линейному виду, МНК применяется к преобразо¬ванным уравнениям. Если в линейной модели и моделях, нели¬нейных по переменным, при оценке параметров исходят из кри¬терия min, то в моделях, нелинейных по оцениваемым параметрам, требование МНК применяется не к исходным дан¬ным результативного признака, а к их преобразованным величи¬нам, т. е.ln y, 1/y. Так, в степенной функции МНК применяется к преобразованному уравнению lny = lnα + β ln x ln ε. Это значит, что оценка параметров основывается на миними¬зации суммы квадратов отклонений в логарифмах. Соответственно если в линейных моделях то в моделях, нелинейных по оцениваемым параметрам, . Вследствие этого оценка параметров оказываются несколько смещенной.
10 № 10 ПОКАЗАТЕЛИ КОРРЕЛЯЦИИ
1. индекс корреляции (R):
Величина данного показателя находится в границах: 0 ≤ R ≤ 1, чем ближе к 1, тем теснее связь рассматриваемых призна¬ков, тем более надежно найденное уравнение регрессии.
2. индекс детерминации используется для проверки существенности в целом ур-ия нелинейной регрессии по F- критерию Фишера:
, где R2- индекс детерминации, n- число наблюдений, m – число параметров при переменной х.
11 МНОЖЕСТВЕННАЯ РЕГРЕССИЯ. СПЕЦИФИКАЦИЯ МОДЕЛИ. ОТБОР ФАКТОРОВ ПРИ ПОСТРОЕНИИИ МОДЕЛИ.
Регрессия может дать хороший результат при модели¬ровании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Поведение отдельных экономи¬ческих переменных контролировать нельзя, т. е. не удается обес¬печить равенство всех прочих условий для оценки влияния одно¬го исследуемого фактора. В этом случае следует попытаться выявить влияние других факторов, введя их в модель, т. е. пост¬роить уравнение множественной регрессии: y=a+b1x1+b2+…+bpxp+e; Такого рода уравнение может использоваться при изучении потребления. Тогда коэффициенты bj — частные производные потребления у по соответствующим факторам xi: , в предположении, что все остальные хi постоянны. В 30-е гг. XX в. Кейнс сформулировал свою гипотезу потребительской функции. С того времени исследователи неод¬нократно обращались к проблеме ее совершенствования. Совре¬менная потребительская функция чаще всего рассматривается как модель вида: C=j(y,P,M,Z), где С — потребление; у — доход; Р — цена, индекс стоимости жизни; М — наличные деньги; Z — ликвидные активы. При этом .. Основная цель множественной регрессии — построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель. Спецификация модели включает в себя два круга вопросов: отбор фак¬торов и выбор вида уравнения регрессии. Требования к факторам.1 Они должны быть количественно измеримы. Если необхо¬димо включить в модель качественный фактор, не имеющий ко¬личественного измерения, то ему нужно придать количествен¬ную определенность (например, в модели урожайности качество почвы задается в виде баллов) 2.Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи. Включение в модель факторов с высокой интеркорреляцией, когда Ryx1 Rx1x2.Для зависимости y=a+b1x1+b2+…+bpxp+e может привести к нежелательным последствиям, повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии. Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются не интерпретированными.
Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной. Если строится модель с набором р-факторов, то для нее рассчитывается показа¬тель детерминации R2 , который фиксирует долю объясненной ва¬риации результативного признака за счет рассматриваемых в ре¬грессии р-факторов. Влияние других не учтенных в модели фак¬торов оценивается как 1 - R2 с соответствующей остаточной дис¬персией S2.При дополнительном включении в регрессию (р + 1) фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться: . Насыщение модели лишними факторами не только не снижа¬ет величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по t-критерию Стьюдента.
Таким образом, хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически в этом нет необходимости. Отбор факторов производится на основе качест¬венного теоретико-экономического анализа, который обычно осуществляется в две стадии: на первой подби¬раются факторы исходя из сущности проблемы; на второй – на основе показателей корреляции определяют t-статистики для параметров регрессии. Коэффициенты интеркорреляции (т. е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменных явно коллинеарны, т. е. находятся между собой в линейной зависимости, если . Ес¬ли факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочте¬ние при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множест¬венной регрессии как метода исследования комплексного воз¬действия факторов в условиях их независимости друг от друга. Наибольшие труд¬ности в использовании аппарата множественной регрессии воз¬никают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимос¬тью. Наличие мультиколлинеарности факторов может озна¬чать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полно¬стью независимой, и нельзя оценить воздействие каждого факто¬ра в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов (МНК). Включение в модель мультиколлинеарных факторов нежела¬тельно в силу следующих последствий:1.затрудняется интерпретация параметров множественной ре¬грессии как характеристик действия факторов в «чистом» ви¬де, ибо факторы коррелированы; параметры линейной регрессии теряют экономический смысл;2оценки параметров ненадежны, обнаруживают большие стан¬дартные ошибки и меняются с изменением объема наблюде¬ний. Для оценки мультиколлинеарности факторов может исполь¬зоваться определитель матрицы парных коэффициентов корреля¬ции между факторами.
Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей. Для включающего три объ¬ясняющих переменных уравнения: y=a+b1x1+b2+b3x3+e.Матрица коэф-в корреляции м/у факторами имела бы определитель равный 1. Det =1, т.к. rx1x1=rx2x2=1 и rx1x2=rx1x3=rx2x3=0. Если м/у факторами сущ-ет полная линейная зависимость и все коэф-ты корреляции =1, то определитель такой матрицы =0. Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной кор¬реляции, тем меньше мультиколлинеарность факторов.
12.Уравнение линейной множественной регрессии, нахождение к-тов модели.
Линейная модель множественной регрессии. У=а0+а1х1+ а2х2+…+ аmхm+e
Параметры определяются с помощью методов наименьших квадратов.
Для этого проведем все рассуждения в матричной форме. Введем следующие матричные обозначения:
;
где У вектор n значений результативного показателя.
Х – матрица n значений m независимых переменных; а матрица параметров
У=Х∙а+ε.
Заметим, что а – выборочные оценки совокупности.
Итак, метод наименьших квадратов требует мин-ии суммы квадратов отклонений исходных модели значений
,
Далее:
Из матричной алгебры известно, что , тогда:
1 – это есть матрица размерностью 1Х1, т.е. число-скаляр, а скаляр при трансформировании не меняется, поэтому
Согласно условию экстремума S по а =0
;
2ХТY+2aXTX=0
XTY=aXTX
Для погашения а умножим обе части этого уравнения на (ХТХ)-1, тогда
а= (XTХ)-1∙XTY
Решение задачи нахождения матицы, а возможно лишь в том случае, если строки и столбцы матрицы Х линейно независимы.
13 множественная корреляция и частичная корреляция
Эк явления как правило определяются большими числами одновременно и совокупно действующих факторов. В связи с этим возникает задача исследования зависимости одной (или нескольких) переменных у от совокупности переменных (х1 х2 … хm). В таком случае для измерения тесноты связи м\у У и факторными признаками хj (j =1 … n) используют множественных коэффициент корреляции.
Для этого используют матрицу парных коэффициентов корреляции м\у всеми рассматриваемыми переменными.
По этой матрице вычисляется множественный коэффициент корреляции, отражающий тесноту связи м/у Y и всеми остальными факторами.
, где R – алгебраические дополнения к соответствующим коэффициентам.
Частный коэффициент корреляции устанавливается зависимость м\у j-ым и k-ым фактором при исключении остальных.
14 НАЗНАЧЕНИЕ ЧАСТНОЙ КОРРЕЛЯЦИИ ПРИ ПОСТРОЕНИИ МОДЕЛИ МНОЖЕСТВЕННОЙ РЕГРЕССИИ. Ранжирование факторов, участву¬ющих во множественной линейной регрессии, может быть прове¬дено через стандартизованные коэффициенты регрессии, с помо¬щью частных коэффициентов корреляции — для линейных связей. При нелинейной взаимосвязи исследуемых признаков эту функцию выполняют частные индексы детерминации. Кроме того, частные показатели корреляции широко используются при решении проблемы отбора факторов: целесообразность включе¬ния того или иного фактора в модель доказывается величиной показателя частной корреляции.
Частные коэффициенты (или индексы) корреляции характери¬зуют тесноту связи между результатом и соответствующим фак¬тором при устранении влияния других факторов, включенных в уравнение регрессии.
Показатели частной корреляции представляют собой отно¬шение сокращения остаточной дисперсии за счет дополнитель¬ного включения в анализ нового фактора к остаточной диспер¬сии, имевшей место до введения его в модель.
Частные коэффициенты корреляции измеряющие влияние на у фактора хi при неизменном уровне др. факторов можно определить по формуле:
;
При двух факторах и i=1 данная формула примет вид:
Частные коэффициенты корреляции изменяются в пределах от -1 до 1.
15/16. ЧАСТНЫЙ F-КРИТЕРИЙ, ЕГО ОТЛИЧИЕ ОТ ПОСЛЕДОВАТЕЛЬНОГО F-КРИТЕРИЯ, СВЯЗЬ МЕЖДУ СОБОЙ t- КРИТЕРИЯ СТЬЮДЕНТА ДЛЯ ОЦЕНКИ ЗНАЧИМОСТИ bi И ЧАСТНЫМ F-КРИТЕРИЕМ.
Ввиду корреляции м/у факторами значимость одного и того же фактора м/б различной в зависимости от последовательности его введения в модель. Мерой для оценки включения фактора в модель служит частый F-критерий, т.е. Fxi. В общем виде для фактора xi частый F-критерий определяется как :
Если рас¬сматривается уравнение y=a+b1x1+b2+b3x3+e, то определяются последовательно F-критерий для уравнения с од¬ним фактором х1, далее F-критерий для дополнительного включе¬ния в модель фактора х2, т. е. для перехода от однофакторного уравнения регрессии к двухфакторному, и, наконец, F-критерий для дополнительного включения в модель фактора х3, т. е. дается оценка значимости фактора х3 после включения в модель факто¬ров x1 их2. В этом случае F-критерий для дополнительного вклю¬чения фактора х2 после х1 является последовательным в отличие от F-критерия для дополнительного включения в модель фактора х3, который является частным F-критерием, ибо оценивает значи¬мость фактора в предположении, что он включен в модель по¬следним. С t-критерием Стьюдента связан именно частный F-критерий. Последовательный F-критерий может интересовать исследователя на стадии формирования модели. Для уравнения y=a+b1x1+b2+b3x3+e оценка значимости коэффициентов регрессии Ь1,Ь2,,b3 предпола¬гает расчет трех межфакторных коэффициентов детерминации, а именно: , , и можно убедиться, что существует связь между собой t- критерия Стьюдента для оценки значимости bi и частным F-критерием:
На основе соотношения bi и получим:
19,20 ПРЕДПОСЫЛКИ МНК.
При оценке параметров уравнения регрессии применяется МНК. При этом делаются определенные предпосылки относительно составляющей , которая представляет собой ненаблюдаемую величину.
Исследования остатков - предполагают проверку наличия сле¬дующих пяти предпосылок МНК:1.случайный характер остатков; 2.нулевая средняя величина остатков, не зависящая от хi;
3.гомоскедастичность—дисперсия каждого отклонения ,одинакова для всех значений х; 4.отсутствие автокорреляции остатков. Значения остатков , распределены независимо друг от друга; 5.остатки подчиняются нормальному распределению.
1. Проверяется случайный характер остатков , с этой целью строится график зависимости остатков от теоретических значений результативного признака. Если на графике получена горизонтальная полоса, то остатки , представляют собой случайные величины и МНК оправдан, те¬оретические значения ух хорошо аппроксимируют фактические значения y. В других случаях необходимо либо применять дру¬гую функцию, либо вводить дополнительную информацию и за¬ново строить уравнение регрессии до тех пор, пока остатки , не будут случайными величинами.
2. Вторая предпосылка МНК относительно нулевой средней ве¬личины остатков означает, что (у — ух) = 0. Это выполнимо для линейных моделей и моделей, нелинейных относительно вклю¬чаемых переменных. С этой целью наряду с изложенным графиком зависимости остатков от теоретических значений ре¬зультативного признака ух строится график зависимости случай¬ных остатков от факторов, включенных в регрессию хi . Если остатки на графике расположены в виде горизонтальной полосы, то они независимы от значений xj. Если же график показывает наличие зависимости и хj то модель неадек¬ватна. Причины неадекватности могут быть разные.
3. В соответствии с третьей предпосылкой МНК требуется, что¬бы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора xj остатки , имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из поля корреляции. Гомоскедастичность остатков означает, что дисперсия остат¬ков - одинакова для каждого значения х.
4.Отсутствие автокор¬реляции остатков, т. е. значения остатков распределены неза¬висимо друг от друга. Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Отсутствие автокорреляции остаточных величин обеспечива¬ет состоятельность и эффективность оценок коэффициентов ре¬грессии
21 СМЫСЛ ОБОБЩЕННОГО МНК.
При нарушении гомоскедастичности и наличии автокорреля¬ции ошибок рекомендуется традиционный МНК заменять обобщенным методом. Обобщенный МНК применяется к преобразованным данным и позволяет получать оценки, которые обладают не только свойством несмещенности, но и имеют меньшие выборочные дисперсии. Обобщенный МНК для корректировки гетерос-ти. В общем виде для уравнения yi=a+bxi+ei при где Ki – коэф-т пропор-ти. Модель примет вид: yi= + xi+ ei . В ней остаточные величины гетероскедастичны. Предполагая в них отсутствие автокорреляции, можно перейти к уравнению с гомоскедастичными остатками, поделив все переменные, зафик¬сированные в ходе i-го наблюдения на . Тогда дисперсия остатков будет величиной постоянной. От регрессии у по х мы перейдем к регрессии на новых переменных: y/ и х/ . Уравнение регрессии примет вид: . По отношению к обычной регрессии уравнение с новыми, преобразованными переменными представляет собой взвешен¬ную регрессию, в которой переменные у и х взяты с весами . Коэф-т регрессии b можно определить как Как видим, при использовании обобщенного МНК с целью корректировки гетероскедастичности коэффициент регрессии b представляет собой взвешенную величину по отношению к обычному МНК с весами 1/К.Аналогичный подход возможен не только для уравнения парной, но и для множественной регрессии. Модель примет вид: . Модель с преобразованными переменными составит
. Это уравнение не содер-т свобод-го члена, применяя обычный МНК получим: Применение в этом случае обобщенного МНК приводит к то¬му, что наблюдения с меньшими значениями преобразованных переменных х/К имеют при определении параметров регрессии относительно больший вес, чем с первоначальными переменны¬ми.
23. 25,26 СИСТЕМЫ ЭКОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ. ПРОБЛЕМА ИДЕНТИФИКАЦИИ.
Сложные экономические процессы описывают с помощью системы взаимосвязанных уравнений. Различают несколько видов систем уравнений: 1. Система независимых уравнений - когда каждая зависимая переменная у рассматривается как функция одного и того же набора факторов х:
y1=a11*x1+a12*x2+…+a1m*xm+e1
yn=an1*x1+an2*x2+…+anm*xm+en
Для решения этой системы и нахождения ее параметров
используется МНК.
2.Система рекурсивных уравнений – когда зависимая переменная у одного уравнения выступает в виде фактора х в другом уравнении:
y1=a11*x1+a12*x2+…+a1m*xm+e1
y2=b21*y1+a21*x1+a22*x2+…+a2m*xm+e2
y3=b31*y1+b32*y2+a31*x1+a32*x2+…+a3m*xm+e3
yn=bn1*y1+bn2*y2+…+bnk-1*yn-1+an1*x1+an2*x2+…+anm*xm+en
Для решения этой системы и нахождения ее параметров используется МНК.
3 Система взаимосвязанных уравнений – когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других – в правую.
y1=b12*y2+b13*y3+…+b1n*yn+a11*x1+a12*x2+…+a1m*xm+e1
y2=b21*y1+b23*y3+…+b2n*yn+a21*x1+a22*x2+…+a2m*xm+e2
yn=bn1*y1+bn2*y2+…+bnk-1*yn-1+an1*x1+an2*x2+…+anm*xm+en
Такая система уравнений называется структурной формой модели. Эндогенные переменные – взаимосвязанные переменные, которые определяются внутри модели (системы) у. Экзогенные переменные – независимые переменные, которые определяются вне системы х. Предопределенные переменные – экзогенные и лаговые (за предыдущие моменты времени) эндогенные переменные системы. Коэффициенты a и b при переменных – структурные коэффициенты модели. Система линейных функций эндогенных переменных от всех предопределенных переменных системы - приведенная форма модели. где - коэффициенты приведенной формы модели.
Необходимое условие идентификации – выполнение счетного правила:
D+1=H –уравнение идентифицируемо;
D+1H – уравнение сверхидентифицируемо.
Где Н – число эндогенных переменных в уравнении, D – число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе.
Достаточное условие идентификации- определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в исследуемом уравнении на равен нулю и ранг этой матрицы не менее эндогенных переменных без единицы. Для решения идентифицируемого уравнения применяется КМНК, для решения сверхидентифицируемых - двухшаговый МНК.
27 Оценивание параметров структурной модели
Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение в литературе получили следующие методы оценивания коэффициентов структурной модели:
• косвенный метод наименьших квадратов (КМНК)
• двухшаговый метод наименьших квадратов (ДМНК)
• трехшаговый метод наименьших квадратов (ТМНК)
• метод максимального правдоподобия с полной информацией (ММП)
• метод максимального правдоподобия при ограниченной информации (ММП)
Косвенный и Двухшаговый методы наименьших квадратов подробно описаны в литературе и рассматриваются как традиционные методы оценки коэффициентов структурной модели. Эти методы достаточно легкореализуемы. Косвенный метод наименьших квадратов применяется для идетифицируемой системы одновременных уравнений, двухшаговый метод наименьших квадратов - для оценки коэффициентов сверхидентифицируемой модели. Перечисленные методы оценивания также используются для сверхидентифицируемых систем уравнений.
Метод максимального правдоподобия рассматривается как наиболее общий метод оценивания, результаты которого при нормальном распределении признаков совпадают с МНК. Однако при большом числе уравнений системы этот метод приводит к достаточно сложным вычислительным процедурам. Поэтому в качестве модификации используется метод максимального правдоподобия при ограниченной информации (метод наименьшего дисперсионного отношения) разработанный в 1949 г. Т. Андерсеном и Н. Рубинным. Математическое описание метода дано, например, в работе Дж. Джонстона. В отличие от метода максимального правдоподобия в данном методе сняты ограничения на параметры, связанные с функционированием системы в целом. Это делает решение более простым, но трудоемкость вычислений остается достаточно высокой. несмотря на его популярность, к середине 1960-х годов он был практически вытеснен двухшаговым методом наименьших квадратов в связи с гораздо большей простотой последнего. Этому способствовала также разработка в 1961 г. Г. Тейлом семейства оценок коэффициентов структурной модели. Для данной модели Г. Тейл определил семейство оценок класса К и обычный МНК при К = 0, ДМНК при К = 1 и метод ограниченной информации при plimK = 1. В последнем случае решение структурной модели соответствует оценкам по ДМНК.
Дальнейшим развитием двухшагового метода наименьших квадратов является трехшаговый МНК (ТМНК), предложенный в 1962 г. А. Зельнером и Г. Тейлом. Этот метод оценивания пригоден для всех видов уравнений структурной модели. Однако при некоторых ограничениях на параметры более эффективным оказывается ДМНК.
28 КМНК. Применяется в случае точно идентифицируемой модели. Процедура применения КМНК предполагает выполнение следующих этапов: 1. Составляют приведенную форму модели и определяют численные значения параметров для каждого ее уравнения обычным МНК. 2. путем алгебраических преобразований переходят от приведенной формы к уравнениям структурной формы модели, получая тем самым численные оценки структурных параметров.
Основная идея ДМНК — на основе приведенной формы модели получить для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения. Далее, подставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифи¬цируемого уравнения. Метод получил название двухшагового МНК, ибо дважды используется МНК: на первом шаге при определении приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной
и на втором шаге применительно к структурному сверхидентифицируемому уравнению при опре¬делении структурных коэффициентов модели по данным теоре¬тических (расчетных) значений эндогенных переменных.
Сверхидентифицируемая структурная модель может быть двух типов:
• все уравнения системы сверхидентифицируемы;
• система содержит наряду со сверхидентифицируемыми точно
идентифицируемые уравнения.
Если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения исполь¬зуется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений.
Применим ДМНК к простейшей сверхидентифицируемой
модели:
Данная модель может быть получена из предыдущей иденти¬фицируемой модели:
если наложить ограничения на ее параметры, а именно: b12 =a11
В результате первое уравнение стало сверхидентифицир
Тэги: александр, гумф, сергеевич, трус, шпора, эконометрика, эконометрике
Есть еще одно занятие - Экзамен по эконометрике сдавать... 2011-10-30 21:54:54
... по ТРУСОВУ Александру Сергеевичу, не если и ...
+ развернуть текст сохранённая копия
Чтоб пусто было тому человеку кто в совершенстве знает эконометрику.... А если её ведет Трусов, то я уверен, что мало кто её знает впринципе =))) Этот пост чисто для меня, ибо сижу как дурак, готовлюсь к экзамену, к предмету которого не знаю... сколько раз я готовился и сдавал подобные сессии... но такой ещё не было. То что иде после черты не обязательно есть в вопросах по ТРУСОВУ Александру Сергеевичу, не если и этого не знать, или хотябы не прочесть то хана. ________________________________________________________________________________________________________________ ________________________________________________________________________________________________________________ 1 Эконометрика — наука, изучающая количественные и качественные экономические взаимосвязи с помощью математических и статистических методов и моделей[1]. Современное определение предмета эконометрики было выработано в уставе Эконометрического общества, которое главными целями назвало использование статистики и математики для развития экономической теории[2]. Теоретическая эконометрика рассматривает статистические свойства оценок и испытаний, в то время как прикладная эконометрика занимается применением эконометрических методов для оценки экономических теорий.
Эконометрический метод складывался в преодолении следующих неприятностей, искажающих результаты применения классических статистических методов:
• асимметричности связей;
• мультиколлинеарности объясняющих переменных;
• закрытости механизма связи между переменными в изолированной регрессии;
• эффекта гетероскедастичности, т. е. отсутствия нормального распределения остатков для регрессионной функции;
• автокорреляции;
• ложной корреляции;
• наличия лагов.
Эконометрическая модель, как правило, основана на теоретическом предположении о круге взаимосвязанных переменных и характере связи между ними. При всем стремлении к «наилучшему» описанию связей приоритет отдается качественному анализу. Поэтому в качестве этапов эконометрического исследования можно указать:
• постановку проблемы;
• получение данных, анализ их качества;
• спецификацию модели;
• оценку параметров;
• интерпретацию результатов.
3. Линейное уравнение регрессии, коэффициенты модели.
Линейная модель парной регрессии есть: у=а0+а1х+
а1 - коэф-т регрессии, показывающий, как изменится у при изменении х на единицу
а0 - это свободный член, расчетная величина, содержания нет.
- это остаточная компонента, т.е. случайная величина, независимая, нормально распределенная, мат ожид = 0 и постоянной дисперсией.
В матричной форме модель имеет вид:
Y=XA+ε
Где Y– вектор-столбец размерности (nx1) наблюдаемых значений зависимой переменной; Х– матрица размерности (nx2) наблюдаемых значений факторных признаков. Дополнительный фактор х0 вводится для вычисления свободного члена; А– вектор-столбец размерности (2х1) неизвестных, подлежащих оценке коэффициентов регрессии; ε– вектор-столбец размерности (nх1) ошибок наблюдений
;
Параметры модели находятся с использованием МНК. Подсчитывается сумма квадратов ошибок наблюдений.
4 ЛИНЕЙНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ: СМЫСЛ И ОЦЕНКА ПАРАМЕТРОВ
Линейная регрессия сводится к нахождению уравнения вида или .
Уравнение вида позволяет по заданным значениям фактора x иметь теоретические значения результативного признака, подставляя в него фактические значения фактора х.
Построение линейной регрессии сводится к оценке ее пара¬метров а и в.
Оценки параметров линейной регрессии могут быть найдены разными методами.
1.
2.
Параметр b называется коэффициентом регрессии. Его вели¬чина показывает среднее изменение результата с изменением фактора на одну единицу.
Формально а — значение у при х = 0. Если признак-фактор
не имеет и не может иметь нулевого значения, то вышеуказанная
трактовка свободного члена, а не имеет смысла. Параметр, а может
не иметь экономического содержания. Попытки экономически
интерпретировать параметр, а могут привести к абсурду, особенно при а < 0.
Интерпретировать можно лишь знак при параметре а. Если а > 0, то относительное изменение результата происходит медленнее, чем изменение фактора.
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции rxy. Существуют разные модификации формулы линейного коэф¬фициента корреляции.
Линейный коэффициент корреляции находится и границах: -1≤.rxy ≤ 1. При этом чем ближе r к 0 тем слабее корреляция и наоборот чем ближе r к 1 или -1, тем сильнее корреляция, т.е. зависимость х и у близка к линейной. Если r в точности =1или -1 все точки лежат на одной прямой. Если коэф. регрессии b>0 то 0 ≤.rxy ≤ 1 и наоборот при b<0 -1≤.rxy ≤0. Коэф. корреляции отражает степени линейной зависимости м/у величинами при наличии ярко выраженной зависимости др. вида.
Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции , называемый коэффициентом детерминации. Коэффициент детермина¬ции характеризует долю дисперсии результативного признака y, объясняемую регрессией. Соответствующая величина характеризует долю дисперсии у, вызванную влиянием остальных не учтенных в модели факторов.
5. ОЦЕНКА СУЩЕСТВЕННОСТИ ПАРАМЕТРОВ ЛИНЕЙНОЙ РЕГРЕССИИ И КОРРЕЛЯЦИИ.
Оценка значимости уравнения регрессии в целом дается с по¬мощью F-критерия Фишера. При этом выдвигается нулевая ги¬потеза, что коэффициент регрессии равен нулю, т. е. b = 0, и следовательно, фактор х не оказывает влияния на результат у.
Непосредственному расчету F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложе¬ние общей суммы квадратов отклонений переменной у от средне го значения у на две части - «объясненную» и «необъясненную»:
- общая сумма квадратов отклонений
- сумма квадратов отклонения объясненная регрессией - остаточная сумма квадратов отклонения.
Любая сумма квадратов отклонений связана с числом степе¬ней свободы, т. е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности nис числом определяемых по ней констант. Применительно к исследуемой проблеме число cтепеней свободы должно показать, сколько независимых откло¬нений из п возможных требуется для образования данной суммы квадратов.
Дисперсия на одну степень свободы D.
F-отношения (F-критерий):
Ecли нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для Н0 необходимо опровержение, чтобы факторная дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором раз¬работаны таблицы критических значений F-отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение F-критерия — это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признается достоверным, если о больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: Fфакт > Fтабл Н0 отклоняется.
Если же величина окажется меньше табличной Fфакт ‹, Fтабл , то вероятность нулевой гипотезы выше заданного уровня и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым. Но не отклоняется.
Стандартная ошибка коэффициента регрессии
Для оценки существенности коэффициента регрессии его ве¬личина сравнивается с его стандартной ошибкой, т. е. определяется фактическое значение t-критерия Стьюдентa: которое
затем сравнивается с табличным значением при определенном уровне значимости и числе степеней свободы (n- 2).
Стандартная ошибка параметра а:
Значимость линейного коэффициента корреляции проверя¬ется на основе величины ошибки коэффициента корреляции тr:
Общая дисперсия признака х:
Коэф. регрессии Его величина показывает ср. изменение результата с изменением фактора на 1 ед.
Ошибка аппроксимации:
6,5. ИНТЕРВАЛЫ ПРОГНОЗА ПО ЛИНЕЙНОМУ УРАВНЕНИЮ РЕГРЕССИИ
Оценка стат. значимости параметров регрессии проводится с помощью t – статистики Стьюдента и путем расчета доверительного интервала для каждого из показателей. Выдвигается гипотеза Н0 о статистически значимом отличие показателей от 0 a = b = r = 0. Рассчитываются стандартные ошибки параметров a,b, r и фактич. знач. t – критерия Стьюдента.
Определяется стат. значимость параметров.
ta ›Tтабл - a стат. значим
tb ›Tтабл - b стат. значим
Находятся границы доверительных интервалов.
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что параметры a и b находясь в указанных границах не принимают нулевых значений, т.е. не явл.. стат. незначимыми и существенно отличается от 0.
7. НЕЛИНЕЙНАЯ РЕГРЕССИЯ. ВИДЫ МОДЕЛЕЙ
Если между экономическими явлениями существуют нели¬нейные соотношения, то они выражаются с помощью соответ¬ствующих нелинейных функций: например, равносторонней ги¬перболы , параболы второй степени и д.р.
Различают два класса нелинейных регрессий:
• регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым па¬раметрам;
• регрессии, нелинейные по оцениваемым параметрам.
Примером нелинейной регрессии по включаемым в нее объ¬ясняющим переменным могут служить следующие функции:
• полиномы разных степеней
• равносторонняя гипербола
К нелинейным регрессиям по оцениваемым параметрам от¬носятся функции:
• степенная
• показательная
экспоненциальная
8,9 ПРИМЕНЕНИЕ МНК К МОДЕЛЯМ НЕЛИНЕЙНЫМ ОТНОСИТЕЛЬНО ВКЛЮЧАЕМЫХ ПЕРЕМЕННЫХ И ОЦЕНИВАЕМЫХ ПАРАМЕТРОВ.
Нелинейная регрессия по включенным переменным не таит каких-либо сложностей в оценке ее параметров. Она определяет¬ся, как и в линейной регрессии, методом наименьших квадратов (МНК), ибо эти функции линейны по параметрам. Так, в парабо¬ле второй степени y=a0+a1x+a2x2+ε заменяя переменные x=x1,x2=x2, получим двухфакторное урав¬нение линейной регрессии: у=а0+а1х1+а2х2+ ε
Парабола второй степени целесообразна к применению, если для определенного интервала значений фактора меняется харак¬тер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую. В этом случае определяется значение фактора, при котором достигается максимальное (или минимальное), значение результативного признака: приравнива¬ем к нулю первую производную параболы второй степени: , т.е. b+2cx=0 и x=-b/2c
Применение МНК для оценки параметров параболы второй степени приводит к следующей системе нормальных уравнений:
Решение ее возможно методом определителей:
В моделях, нелинейных по оцениваемым параметрам, но приводимых к линейному виду, МНК применяется к преобразо¬ванным уравнениям. Если в линейной модели и моделях, нели¬нейных по переменным, при оценке параметров исходят из кри¬терия min, то в моделях, нелинейных по оцениваемым параметрам, требование МНК применяется не к исходным дан¬ным результативного признака, а к их преобразованным величи¬нам, т. е.ln y, 1/y. Так, в степенной функции МНК применяется к преобразованному уравнению lny = lnα + β ln x ln ε. Это значит, что оценка параметров основывается на миними¬зации суммы квадратов отклонений в логарифмах. Соответственно если в линейных моделях то в моделях, нелинейных по оцениваемым параметрам, . Вследствие этого оценка параметров оказываются несколько смещенной.
10 № 10 ПОКАЗАТЕЛИ КОРРЕЛЯЦИИ
1. индекс корреляции (R):
Величина данного показателя находится в границах: 0 ≤ R ≤ 1, чем ближе к 1, тем теснее связь рассматриваемых призна¬ков, тем более надежно найденное уравнение регрессии.
2. индекс детерминации используется для проверки существенности в целом ур-ия нелинейной регрессии по F- критерию Фишера:
, где R2- индекс детерминации, n- число наблюдений, m – число параметров при переменной х.
11 МНОЖЕСТВЕННАЯ РЕГРЕССИЯ. СПЕЦИФИКАЦИЯ МОДЕЛИ. ОТБОР ФАКТОРОВ ПРИ ПОСТРОЕНИИИ МОДЕЛИ.
Регрессия может дать хороший результат при модели¬ровании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Поведение отдельных экономи¬ческих переменных контролировать нельзя, т. е. не удается обес¬печить равенство всех прочих условий для оценки влияния одно¬го исследуемого фактора. В этом случае следует попытаться выявить влияние других факторов, введя их в модель, т. е. пост¬роить уравнение множественной регрессии: y=a+b1x1+b2+…+bpxp+e; Такого рода уравнение может использоваться при изучении потребления. Тогда коэффициенты bj — частные производные потребления у по соответствующим факторам xi: , в предположении, что все остальные хi постоянны. В 30-е гг. XX в. Кейнс сформулировал свою гипотезу потребительской функции. С того времени исследователи неод¬нократно обращались к проблеме ее совершенствования. Совре¬менная потребительская функция чаще всего рассматривается как модель вида: C=j(y,P,M,Z), где С — потребление; у — доход; Р — цена, индекс стоимости жизни; М — наличные деньги; Z — ликвидные активы. При этом .. Основная цель множественной регрессии — построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель. Спецификация модели включает в себя два круга вопросов: отбор фак¬торов и выбор вида уравнения регрессии. Требования к факторам.1 Они должны быть количественно измеримы. Если необхо¬димо включить в модель качественный фактор, не имеющий ко¬личественного измерения, то ему нужно придать количествен¬ную определенность (например, в модели урожайности качество почвы задается в виде баллов) 2.Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи. Включение в модель факторов с высокой интеркорреляцией, когда Ryx1 Rx1x2.Для зависимости y=a+b1x1+b2+…+bpxp+e может привести к нежелательным последствиям, повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии. Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются не интерпретированными.
Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной. Если строится модель с набором р-факторов, то для нее рассчитывается показа¬тель детерминации R2 , который фиксирует долю объясненной ва¬риации результативного признака за счет рассматриваемых в ре¬грессии р-факторов. Влияние других не учтенных в модели фак¬торов оценивается как 1 - R2 с соответствующей остаточной дис¬персией S2.При дополнительном включении в регрессию (р + 1) фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться: . Насыщение модели лишними факторами не только не снижа¬ет величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по t-критерию Стьюдента.
Таким образом, хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически в этом нет необходимости. Отбор факторов производится на основе качест¬венного теоретико-экономического анализа, который обычно осуществляется в две стадии: на первой подби¬раются факторы исходя из сущности проблемы; на второй – на основе показателей корреляции определяют t-статистики для параметров регрессии. Коэффициенты интеркорреляции (т. е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменных явно коллинеарны, т. е. находятся между собой в линейной зависимости, если . Ес¬ли факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочте¬ние при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множест¬венной регрессии как метода исследования комплексного воз¬действия факторов в условиях их независимости друг от друга. Наибольшие труд¬ности в использовании аппарата множественной регрессии воз¬никают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимос¬тью. Наличие мультиколлинеарности факторов может озна¬чать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полно¬стью независимой, и нельзя оценить воздействие каждого факто¬ра в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов (МНК). Включение в модель мультиколлинеарных факторов нежела¬тельно в силу следующих последствий:1.затрудняется интерпретация параметров множественной ре¬грессии как характеристик действия факторов в «чистом» ви¬де, ибо факторы коррелированы; параметры линейной регрессии теряют экономический смысл;2оценки параметров ненадежны, обнаруживают большие стан¬дартные ошибки и меняются с изменением объема наблюде¬ний. Для оценки мультиколлинеарности факторов может исполь¬зоваться определитель матрицы парных коэффициентов корреля¬ции между факторами.
Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей. Для включающего три объ¬ясняющих переменных уравнения: y=a+b1x1+b2+b3x3+e.Матрица коэф-в корреляции м/у факторами имела бы определитель равный 1. Det =1, т.к. rx1x1=rx2x2=1 и rx1x2=rx1x3=rx2x3=0. Если м/у факторами сущ-ет полная линейная зависимость и все коэф-ты корреляции =1, то определитель такой матрицы =0. Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной кор¬реляции, тем меньше мультиколлинеарность факторов.
12.Уравнение линейной множественной регрессии, нахождение к-тов модели.
Линейная модель множественной регрессии. У=а0+а1х1+ а2х2+…+ аmхm+e
Параметры определяются с помощью методов наименьших квадратов.
Для этого проведем все рассуждения в матричной форме. Введем следующие матричные обозначения:
;
где У вектор n значений результативного показателя.
Х – матрица n значений m независимых переменных; а матрица параметров
У=Х∙а+ε.
Заметим, что а – выборочные оценки совокупности.
Итак, метод наименьших квадратов требует мин-ии суммы квадратов отклонений исходных модели значений
,
Далее:
Из матричной алгебры известно, что , тогда:
1 – это есть матрица размерностью 1Х1, т.е. число-скаляр, а скаляр при трансформировании не меняется, поэтому
Согласно условию экстремума S по а =0
;
2ХТY+2aXTX=0
XTY=aXTX
Для погашения а умножим обе части этого уравнения на (ХТХ)-1, тогда
а= (XTХ)-1∙XTY
Решение задачи нахождения матицы, а возможно лишь в том случае, если строки и столбцы матрицы Х линейно независимы.
13 множественная корреляция и частичная корреляция
Эк явления как правило определяются большими числами одновременно и совокупно действующих факторов. В связи с этим возникает задача исследования зависимости одной (или нескольких) переменных у от совокупности переменных (х1 х2 … хm). В таком случае для измерения тесноты связи м\у У и факторными признаками хj (j =1 … n) используют множественных коэффициент корреляции.
Для этого используют матрицу парных коэффициентов корреляции м\у всеми рассматриваемыми переменными.
По этой матрице вычисляется множественный коэффициент корреляции, отражающий тесноту связи м/у Y и всеми остальными факторами.
, где R – алгебраические дополнения к соответствующим коэффициентам.
Частный коэффициент корреляции устанавливается зависимость м\у j-ым и k-ым фактором при исключении остальных.
14 НАЗНАЧЕНИЕ ЧАСТНОЙ КОРРЕЛЯЦИИ ПРИ ПОСТРОЕНИИ МОДЕЛИ МНОЖЕСТВЕННОЙ РЕГРЕССИИ. Ранжирование факторов, участву¬ющих во множественной линейной регрессии, может быть прове¬дено через стандартизованные коэффициенты регрессии, с помо¬щью частных коэффициентов корреляции — для линейных связей. При нелинейной взаимосвязи исследуемых признаков эту функцию выполняют частные индексы детерминации. Кроме того, частные показатели корреляции широко используются при решении проблемы отбора факторов: целесообразность включе¬ния того или иного фактора в модель доказывается величиной показателя частной корреляции.
Частные коэффициенты (или индексы) корреляции характери¬зуют тесноту связи между результатом и соответствующим фак¬тором при устранении влияния других факторов, включенных в уравнение регрессии.
Показатели частной корреляции представляют собой отно¬шение сокращения остаточной дисперсии за счет дополнитель¬ного включения в анализ нового фактора к остаточной диспер¬сии, имевшей место до введения его в модель.
Частные коэффициенты корреляции измеряющие влияние на у фактора хi при неизменном уровне др. факторов можно определить по формуле:
;
При двух факторах и i=1 данная формула примет вид:
Частные коэффициенты корреляции изменяются в пределах от -1 до 1.
15/16. ЧАСТНЫЙ F-КРИТЕРИЙ, ЕГО ОТЛИЧИЕ ОТ ПОСЛЕДОВАТЕЛЬНОГО F-КРИТЕРИЯ, СВЯЗЬ МЕЖДУ СОБОЙ t- КРИТЕРИЯ СТЬЮДЕНТА ДЛЯ ОЦЕНКИ ЗНАЧИМОСТИ bi И ЧАСТНЫМ F-КРИТЕРИЕМ.
Ввиду корреляции м/у факторами значимость одного и того же фактора м/б различной в зависимости от последовательности его введения в модель. Мерой для оценки включения фактора в модель служит частый F-критерий, т.е. Fxi. В общем виде для фактора xi частый F-критерий определяется как :
Если рас¬сматривается уравнение y=a+b1x1+b2+b3x3+e, то определяются последовательно F-критерий для уравнения с од¬ним фактором х1, далее F-критерий для дополнительного включе¬ния в модель фактора х2, т. е. для перехода от однофакторного уравнения регрессии к двухфакторному, и, наконец, F-критерий для дополнительного включения в модель фактора х3, т. е. дается оценка значимости фактора х3 после включения в модель факто¬ров x1 их2. В этом случае F-критерий для дополнительного вклю¬чения фактора х2 после х1 является последовательным в отличие от F-критерия для дополнительного включения в модель фактора х3, который является частным F-критерием, ибо оценивает значи¬мость фактора в предположении, что он включен в модель по¬следним. С t-критерием Стьюдента связан именно частный F-критерий. Последовательный F-критерий может интересовать исследователя на стадии формирования модели. Для уравнения y=a+b1x1+b2+b3x3+e оценка значимости коэффициентов регрессии Ь1,Ь2,,b3 предпола¬гает расчет трех межфакторных коэффициентов детерминации, а именно: , , и можно убедиться, что существует связь между собой t- критерия Стьюдента для оценки значимости bi и частным F-критерием:
На основе соотношения bi и получим:
19,20 ПРЕДПОСЫЛКИ МНК.
При оценке параметров уравнения регрессии применяется МНК. При этом делаются определенные предпосылки относительно составляющей , которая представляет собой ненаблюдаемую величину.
Исследования остатков - предполагают проверку наличия сле¬дующих пяти предпосылок МНК:1.случайный характер остатков; 2.нулевая средняя величина остатков, не зависящая от хi;
3.гомоскедастичность—дисперсия каждого отклонения ,одинакова для всех значений х; 4.отсутствие автокорреляции остатков. Значения остатков , распределены независимо друг от друга; 5.остатки подчиняются нормальному распределению.
1. Проверяется случайный характер остатков , с этой целью строится график зависимости остатков от теоретических значений результативного признака. Если на графике получена горизонтальная полоса, то остатки , представляют собой случайные величины и МНК оправдан, те¬оретические значения ух хорошо аппроксимируют фактические значения y. В других случаях необходимо либо применять дру¬гую функцию, либо вводить дополнительную информацию и за¬ново строить уравнение регрессии до тех пор, пока остатки , не будут случайными величинами.
2. Вторая предпосылка МНК относительно нулевой средней ве¬личины остатков означает, что (у — ух) = 0. Это выполнимо для линейных моделей и моделей, нелинейных относительно вклю¬чаемых переменных. С этой целью наряду с изложенным графиком зависимости остатков от теоретических значений ре¬зультативного признака ух строится график зависимости случай¬ных остатков от факторов, включенных в регрессию хi . Если остатки на графике расположены в виде горизонтальной полосы, то они независимы от значений xj. Если же график показывает наличие зависимости и хj то модель неадек¬ватна. Причины неадекватности могут быть разные.
3. В соответствии с третьей предпосылкой МНК требуется, что¬бы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора xj остатки , имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из поля корреляции. Гомоскедастичность остатков означает, что дисперсия остат¬ков - одинакова для каждого значения х.
4.Отсутствие автокор¬реляции остатков, т. е. значения остатков распределены неза¬висимо друг от друга. Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Отсутствие автокорреляции остаточных величин обеспечива¬ет состоятельность и эффективность оценок коэффициентов ре¬грессии
21 СМЫСЛ ОБОБЩЕННОГО МНК.
При нарушении гомоскедастичности и наличии автокорреля¬ции ошибок рекомендуется традиционный МНК заменять обобщенным методом. Обобщенный МНК применяется к преобразованным данным и позволяет получать оценки, которые обладают не только свойством несмещенности, но и имеют меньшие выборочные дисперсии. Обобщенный МНК для корректировки гетерос-ти. В общем виде для уравнения yi=a+bxi+ei при где Ki – коэф-т пропор-ти. Модель примет вид: yi= + xi+ ei . В ней остаточные величины гетероскедастичны. Предполагая в них отсутствие автокорреляции, можно перейти к уравнению с гомоскедастичными остатками, поделив все переменные, зафик¬сированные в ходе i-го наблюдения на . Тогда дисперсия остатков будет величиной постоянной. От регрессии у по х мы перейдем к регрессии на новых переменных: y/ и х/ . Уравнение регрессии примет вид: . По отношению к обычной регрессии уравнение с новыми, преобразованными переменными представляет собой взвешен¬ную регрессию, в которой переменные у и х взяты с весами . Коэф-т регрессии b можно определить как Как видим, при использовании обобщенного МНК с целью корректировки гетероскедастичности коэффициент регрессии b представляет собой взвешенную величину по отношению к обычному МНК с весами 1/К.Аналогичный подход возможен не только для уравнения парной, но и для множественной регрессии. Модель примет вид: . Модель с преобразованными переменными составит
. Это уравнение не содер-т свобод-го члена, применяя обычный МНК получим: Применение в этом случае обобщенного МНК приводит к то¬му, что наблюдения с меньшими значениями преобразованных переменных х/К имеют при определении параметров регрессии относительно больший вес, чем с первоначальными переменны¬ми.
23. 25,26 СИСТЕМЫ ЭКОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ. ПРОБЛЕМА ИДЕНТИФИКАЦИИ.
Сложные экономические процессы описывают с помощью системы взаимосвязанных уравнений. Различают несколько видов систем уравнений: 1. Система независимых уравнений - когда каждая зависимая переменная у рассматривается как функция одного и того же набора факторов х:
y1=a11*x1+a12*x2+…+a1m*xm+e1
yn=an1*x1+an2*x2+…+anm*xm+en
Для решения этой системы и нахождения ее параметров
используется МНК.
2.Система рекурсивных уравнений – когда зависимая переменная у одного уравнения выступает в виде фактора х в другом уравнении:
y1=a11*x1+a12*x2+…+a1m*xm+e1
y2=b21*y1+a21*x1+a22*x2+…+a2m*xm+e2
y3=b31*y1+b32*y2+a31*x1+a32*x2+…+a3m*xm+e3
yn=bn1*y1+bn2*y2+…+bnk-1*yn-1+an1*x1+an2*x2+…+anm*xm+en
Для решения этой системы и нахождения ее параметров используется МНК.
3 Система взаимосвязанных уравнений – когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других – в правую.
y1=b12*y2+b13*y3+…+b1n*yn+a11*x1+a12*x2+…+a1m*xm+e1
y2=b21*y1+b23*y3+…+b2n*yn+a21*x1+a22*x2+…+a2m*xm+e2
yn=bn1*y1+bn2*y2+…+bnk-1*yn-1+an1*x1+an2*x2+…+anm*xm+en
Такая система уравнений называется структурной формой модели. Эндогенные переменные – взаимосвязанные переменные, которые определяются внутри модели (системы) у. Экзогенные переменные – независимые переменные, которые определяются вне системы х. Предопределенные переменные – экзогенные и лаговые (за предыдущие моменты времени) эндогенные переменные системы. Коэффициенты a и b при переменных – структурные коэффициенты модели. Система линейных функций эндогенных переменных от всех предопределенных переменных системы - приведенная форма модели. где - коэффициенты приведенной формы модели.
Необходимое условие идентификации – выполнение счетного правила:
D+1=H –уравнение идентифицируемо;
D+1H – уравнение сверхидентифицируемо.
Где Н – число эндогенных переменных в уравнении, D – число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе.
Достаточное условие идентификации- определитель матрицы, составленной из коэффициентов при переменных, отсутствующих в исследуемом уравнении на равен нулю и ранг этой матрицы не менее эндогенных переменных без единицы. Для решения идентифицируемого уравнения применяется КМНК, для решения сверхидентифицируемых - двухшаговый МНК.
27 Оценивание параметров структурной модели
Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение в литературе получили следующие методы оценивания коэффициентов структурной модели:
• косвенный метод наименьших квадратов (КМНК)
• двухшаговый метод наименьших квадратов (ДМНК)
• трехшаговый метод наименьших квадратов (ТМНК)
• метод максимального правдоподобия с полной информацией (ММП)
• метод максимального правдоподобия при ограниченной информации (ММП)
Косвенный и Двухшаговый методы наименьших квадратов подробно описаны в литературе и рассматриваются как традиционные методы оценки коэффициентов структурной модели. Эти методы достаточно легкореализуемы. Косвенный метод наименьших квадратов применяется для идетифицируемой системы одновременных уравнений, двухшаговый метод наименьших квадратов - для оценки коэффициентов сверхидентифицируемой модели. Перечисленные методы оценивания также используются для сверхидентифицируемых систем уравнений.
Метод максимального правдоподобия рассматривается как наиболее общий метод оценивания, результаты которого при нормальном распределении признаков совпадают с МНК. Однако при большом числе уравнений системы этот метод приводит к достаточно сложным вычислительным процедурам. Поэтому в качестве модификации используется метод максимального правдоподобия при ограниченной информации (метод наименьшего дисперсионного отношения) разработанный в 1949 г. Т. Андерсеном и Н. Рубинным. Математическое описание метода дано, например, в работе Дж. Джонстона. В отличие от метода максимального правдоподобия в данном методе сняты ограничения на параметры, связанные с функционированием системы в целом. Это делает решение более простым, но трудоемкость вычислений остается достаточно высокой. несмотря на его популярность, к середине 1960-х годов он был практически вытеснен двухшаговым методом наименьших квадратов в связи с гораздо большей простотой последнего. Этому способствовала также разработка в 1961 г. Г. Тейлом семейства оценок коэффициентов структурной модели. Для данной модели Г. Тейл определил семейство оценок класса К и обычный МНК при К = 0, ДМНК при К = 1 и метод ограниченной информации при plimK = 1. В последнем случае решение структурной модели соответствует оценкам по ДМНК.
Дальнейшим развитием двухшагового метода наименьших квадратов является трехшаговый МНК (ТМНК), предложенный в 1962 г. А. Зельнером и Г. Тейлом. Этот метод оценивания пригоден для всех видов уравнений структурной модели. Однако при некоторых ограничениях на параметры более эффективным оказывается ДМНК.
28 КМНК. Применяется в случае точно идентифицируемой модели. Процедура применения КМНК предполагает выполнение следующих этапов: 1. Составляют приведенную форму модели и определяют численные значения параметров для каждого ее уравнения обычным МНК. 2. путем алгебраических преобразований переходят от приведенной формы к уравнениям структурной формы модели, получая тем самым численные оценки структурных параметров.
Основная идея ДМНК — на основе приведенной формы модели получить для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения. Далее, подставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифи¬цируемого уравнения. Метод получил название двухшагового МНК, ибо дважды используется МНК: на первом шаге при определении приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной
и на втором шаге применительно к структурному сверхидентифицируемому уравнению при опре¬делении структурных коэффициентов модели по данным теоре¬тических (расчетных) значений эндогенных переменных.
Сверхидентифицируемая структурная модель может быть двух типов:
• все уравнения системы сверхидентифицируемы;
• система содержит наряду со сверхидентифицируемыми точно
идентифицируемые уравнения.
Если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения исполь¬зуется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений.
Применим ДМНК к простейшей сверхидентифицируемой
модели:
Данная модель может быть получена из предыдущей иденти¬фицируемой модели:
если наложить ограничения на ее параметры, а именно: b12 =a11
В результате первое уравнение стало сверхидентифицируемым: Н=1 (у1),
D=1(х2) и D+1 > Н. Второе уравнение не изме¬нилось и является точно идентифицируемым: Н = 2 и D=1
На первом шаге найдем приведенную форму модели, а
именно:
ДМНК является наиболее общим и широко распространен¬ным методом решения системы одновременных уравнений.
Несмотря на важность системы эконометрических уравнений, на практике часто не принимают во внимание некоторые взаимосвязи, применение традиционного МНК к одному или нескольким уравнениям также широко распространено в эконометрике. В частности, при построении производственных функций анализ спроса можно вести, используя обычный МНК.
29 ОСНОВНЫЕ ЭЛЕМЕНТЫ ВРЕМЕННОГО РЯДА.
Временной ряд — это совокупность значений какого-либо по¬казателя за несколько последовательных моментов или периодов времени. Каждый уровень временного ряда формируется под воздействие
Тэги: александр, гумф, сергеевич, трус, шпора, эконометрика, эконометрике
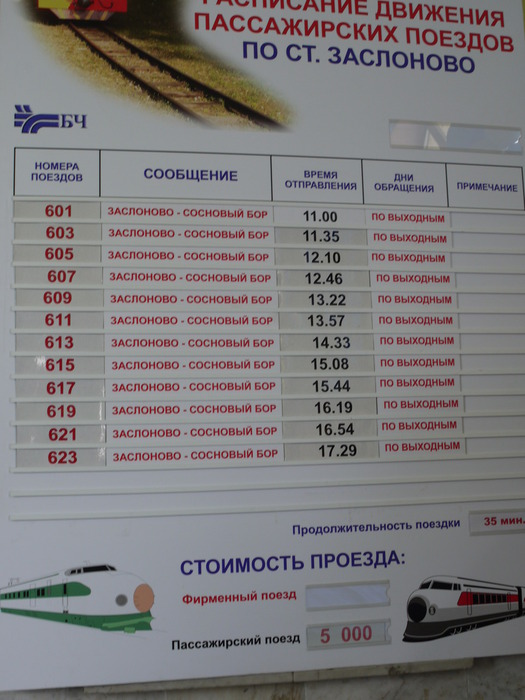
Минск. Детская железная дорога. 2011-07-18 12:45:55
... > Заслонов Константин Сергеевич, в честь которого ...
+ развернуть текст сохранённая копия
Минская детская железная дорога им.К.С.Заслонова, открывшаяся в 1955 году - это четыре километра и полчаса пути, две станции, одна платформа, 2 переезда, мост через речку и путепровод. По ней "бегают" смешные маленькие тепловозики с разрисованными вагончиками. Дорогу называют "малая белорусская" потому, что она точь-в-точь настоящая, перевозит 57 тысяч пассажиров в год, на ней учатся работать юные железнодорожники. Машинисты, проводники, начальники и работники станций - это все детишки из училища, такие серьезные, такие деловые - проверяют билеты, осматривают вагоны на станции - одеты в форму. На станции и в вагонах играют детские песни, бродят сказочные персонажи, есть игрушечная электрическая модель и еще много всего развлекательного, бывают концерты и даже новогодние утренники.
Заслонов Константин Сергеевич, в честь которого названа детская железная дорога - один из руководителей партизанского движения во время ВОВ, русский, Герой Советского Союза, псевдоним - Дядя Костя. До войны он работал как раз на железной дороге - сначала начальником паровозного депо, затем начальником станции, по личной просьбе был направлен в тыл врага в составе группы железнодорожников. Создал подпольную группу, которая совершила ряд успешных диверсий на ж.д, уничтожили массу техники и солдат, погиб в бою с карателями.

Тэги: беларускае!, белорусский, детский, дорога, достопримечательность, железнодорожный, железный, заслон, заслоново, константин, купляйце, малый, минска, минский, минску., путеводитель, сергеевич, учить
Страницы: 1 2 3 4 5 6 7 8 9 10
Главная / Главные темы / Тэг «сергеевич»
|
Взлеты Топ 5
Падения Топ 5
|