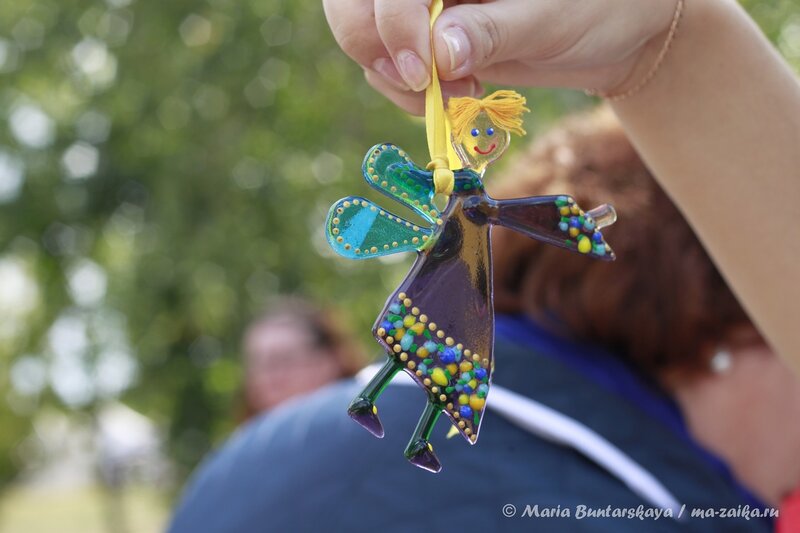Какой рейтинг вас больше интересует?
|
Главная / Главные темы / Тэг «maeda»

Решение адского гроба номер 5 2013-09-10 15:01:54
Решение адского гроба номер 5 из вчерашней контрольной (кину сюда, чтоб не забыть). Что ...
+ развернуть текст сохранённая копия
Решение адского гроба номер 5 из вчерашней контрольной (кину сюда, чтоб не забыть). Что это гроб, было сразу ясно из количества баллов за нее, но гробы всегда хорошо. \задача Пусть $\phi:\; \R\arrow \R^3$ непрерывное, инъективное отображение. Докажите, что $\R^3\backslash \im \phi$ связно, или найдите контрпример. Решение.
Представим $\R$ в виде счетного объединения компактов.
Обозначим за $C$ образ $\phi$ на одном из этих компактов.
Поскольку ограничение $\phi$ на компакт есть гомеоморфизм на образ,
для каждой гиперплоскости $W$ ее пересечение с $C$ -- замкнутое
подмножество $C_W$ в $\R$. Поскольку это пересечение может
иметь ненулевую меру только для счетного числа плоскостей,
$C_W$ для всех $W$, кроме счетного числа - канторовское
множество (вполне несвязное, компактное подмножество в $\R$).
Осталось доказать, что дополнение $\R^2$ к канторовскому
подмножеству (или счетному объединению их) связно.
Обозначим за $U_W$ дополнение $W$ к $C_W$.
Поскольку $U_W$ открыто, линейная связность
совпадает с обычной, и $U_W$ есть объединение
счетного числа открытых компонент связности.
Пусть $U$ -- одна из компонент связности в $U_W$,
а $\6 U$ ее граница, то есть дополнение в замыкании.
Поскольку $\6 U\subset C_W$, осталось доказать,
что оно не канторовское. Можно считать $U$ односвязным,
заклеив все дыры в нем; тогда это диск, и непустое подмножество
в $\6 U$ получается как предел окружностей увеличивающегося
радиуса, то есть это кривая, а значит связное множество.
Привет
 Comments Comments
Тэги: hse, math
[Из песочницы] Sublime Text Vintage Mode — справочник по горячим клавишам 2013-09-10 12:01:25
Как увидел Vintage Mode в действии сразу захотелось научиться им владеть. Как раз к этому времени я ...
+ развернуть текст сохранённая копия
Как увидел Vintage Mode в действии сразу захотелось научиться им владеть. Как раз к этому времени я прошел курс Соло + VerseQ для слепого печатания на английском. Связка с Vintage Mode, мне казалось, будет очень эффективной для верстки, и я не ошибся.
 Для тех кто не знает Vintage Mode (Insert Mode в VIM) плагин для Sublime Text, который идет в комплекте с редактором. Взят он из редактора VIM, и многие думают, что пользу он может принести только бывшим пользователям Vim, но это ошибочное мнение. По умолчанию плагин деактивирован, как активировать объяснять не буду инструкция есть здесь. Скажу только что для входа в режим Vintage используется клавиша i, а для выхода ESC. По моему это крайне неудобно. Я воспользовался советом из оффициальной документации и теперь вхожу в Vintage Mode два раза нажав клавишу i. Подробности тут.
Вроде все отлично осталось только узнать список команд для каждой клавиши, немного понервничать, привыкнуть и готово. Но в официальной документации информации по клавишам нет, они обосновывают это тем, что клавиши те же что и в редакторе Vim. Но различия есть и их немало, документации на русском вообще нет ни по одному из редакторов (именно по Hotkeys Vintage Mode). Читать дальше →
Тэги: mode, sublime, text, vintage, веб-разработка, софт
первую лекцию по векторным расслоениям 2013-09-10 00:07:47
Читал сегодня первую лекцию из осеннего курса по векторным расслоениям, в основном про пучки, и ...
+ развернуть текст сохранённая копия
Читал сегодня первую лекцию из осеннего курса по векторным расслоениям, в основном про пучки, и немного про 1-коциклы. Слайды http://verbit.ru/MATH/BUNDLES-2013/slid es-bun-01.pdf Листочки http://verbit.ru/MATH/BUNDLES-2013/list ok-bun-01.pdf Ну и до кучи, контрольная http://verbit.ru/MATH/BUNDLES-2013/kont r-1.pdf Со временем, нарисую отдельную страничку для курса, а сейчас пусть так повисит. Привет  Comments Comments
Тэги: hse, math
Ergodic complex structures and Kobayashi metric 2013-09-08 16:17:52
Кстати, сходил проголосовал. Чего и вам желаю. Ну и чтобы два раза не вставать, слайды с ...
+ развернуть текст сохранённая копия
Кстати, сходил проголосовал. Чего и вам желаю. Ну и чтобы два раза не вставать, слайды с лекции из семинара в Жуссью: http://verbit.ru/MATH/TALKS/Ergo-ENS-Se p-06-2013.pdf Физически оно было, однако, в Ecole Normale, причем в таком месте, куда я бы никогда пройти не смог, без сопровождающего, потому что там адский лабиринт и черт ногу сломит. Привет  Comments Comments
Тэги: math, travel
С соколовогорской ярмарки hand made (Саратов, 07.09.13) 2013-09-08 11:06:16
< ...
+ развернуть текст сохранённая копия
Тэги: hand, made, волге, города, день, деревня, жизни, история, культура, мастерство, национальная, один, парк, победы, продажи, проспект, реконструкция, рукоделие, саратов, ярмарка
Главная / Главные темы / Тэг «maeda»
Взлеты Топ 5
Падения Топ 5
|
Загрузка... 
|

 Для тех кто не знает Vintage Mode (Insert Mode в VIM) плагин для Sublime Text, который идет в комплекте с редактором. Взят он из редактора VIM, и многие думают, что пользу он может принести только бывшим пользователям Vim, но это ошибочное мнение. По умолчанию плагин деактивирован, как активировать объяснять не буду инструкция есть здесь. Скажу только что для входа в режим Vintage используется клавиша i, а для выхода ESC. По моему это крайне неудобно. Я воспользовался советом из оффициальной документации и теперь вхожу в Vintage Mode два раза нажав клавишу i. Подробности тут.
Для тех кто не знает Vintage Mode (Insert Mode в VIM) плагин для Sublime Text, который идет в комплекте с редактором. Взят он из редактора VIM, и многие думают, что пользу он может принести только бывшим пользователям Vim, но это ошибочное мнение. По умолчанию плагин деактивирован, как активировать объяснять не буду инструкция есть здесь. Скажу только что для входа в режим Vintage используется клавиша i, а для выхода ESC. По моему это крайне неудобно. Я воспользовался советом из оффициальной документации и теперь вхожу в Vintage Mode два раза нажав клавишу i. Подробности тут.