|
Какой рейтинг вас больше интересует?
|
Главная /
Каталог блоговCтраница блогера Смарт Текнолоджис. Мы инженеры и разработчики. Это наш блог./Записи в блоге | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Смарт Текнолоджис. Мы инженеры и разработчики. Это наш блог.
Голосов: 0 Адрес блога: http://smartnlg.blogspot.com/ Добавлен: 2013-03-25 21:58:23 |
|

Критерий качества организации системы
Напомним, что в первой части мы рассмотрели основные особенности самоорганизующихся систем.
Интуитивно, отсутствие организации отождествляется с хаосом. На основании этой интуитивной предпосылки, в кибернетике появилось специфическое понятие организации, которое применимо к широкому кругу объектов и систем и дает численную меру статистических связей между элементами системы - R.
Интуитивно, отсутствие организации отождествляется с хаосом. На основании этой интуитивной предпосылки, в кибернетике появилось специфическое понятие организации, которое применимо к широкому кругу объектов и систем и дает численную меру статистических связей между элементами системы - R.
Это понятие основано на следующих рассуждениях. Пусть имеется некая система, которая состоит из отдельных частей или подсистем (не обязательно однородных). Каждая из этих подсистем, в процессе их существования или деятельности может принимать некоторое множество состояний, над которым задано конкретное распределение вероятностей.
Если все подсистемы разобщены, то есть поведение одной подсистемы никак не влияет на поведение других, или, иными словами, все подсистемы независимы, то система будет являться предельно неорганизованной.
Другой предельный (идеальный) случай – когда состояние одной подсистемы однозначно определяет состояние всех остальных.
Если подсистемы разобщены, то энтропия множества состояний каждой подсистемы Zможет быть определена следующим образом:
H(Z) = - 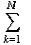 Pk log2 Pk(2.1)
Pk log2 Pk(2.1)
где k= 1, 2, … N– возможные состояния подсистемы Zi, а Pik– вероятность того, что эта подсистема окажется в состоянии k. При этом если Pk=0.5, то
- H(Z) = log2N(2.2)
В предельно неорганизованной системе общая энтропия будет максимальна и равна сумме энтропий её подсистем. Так, для системы, состоящей из двух подсистем – Z*и Z**, будем иметь:
- H0 (Z*, Z**) = H (Z*) + H (Z**)(2.3)
Если в системе имеются связи между её элементами (подсистемами), то есть эти элементы взаимно влияют друг на друга, то система организуется, и общая энтропия становится меньше суммы энтропий её элементов, и будет составлять:
- H1 (Z*, Z**) = H (Z**) + H (Z*|Z**) = H (Z*) + H (Z**|Z*)(2.4)
где H(Z*|Z**) – условная энтропия, которая определяется выражением:
- H (Z*|Z**) = -
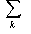 P(Zk**)
P(Zk**) 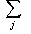 P(Zj *|Zk**) log2 P(Zj *|Zk**)(2.5)
P(Zj *|Zk**) log2 P(Zj *|Zk**)(2.5)
где P(Zj*|Zk**) – вероятность состояния Zj*, если имеет место состояние Zk**.
Величина H(Z*|Z**) всегда удовлетворяет следующему условию:
- 0 H (Z*|Z**) H (Z*)(2.6)
при этом величина H(Z*|Z**)=0 только в том случае, если каждое состояние Zj* однозначно определяется состоянием Zk**. При таких условиях все P(Zj*|Zk**)=1, и H(Z*|Z**)=0 (в силу того, что log1=0). Данный случай соответствуют идеальной организации системы.
Таким образом, в результате организации системы её энтропия H1будет ниже максимальной энтропии H0. Это уменьшение энтропии может служить численной мерой организованности системы – R:
- R = H0 – H1 = H (Z*) - H(Z*|Z**)(2.7)
при этом величина R=0 будет соответствовать предельно неорганизованной системе, а величина R=Н(Z*) – системе, которая организована идеально.
Следует отметить, что величина Rопределяет уровень организации системы в процессе её функционирования (в динамике), а именно: величина Rможет быть больше нуля только тогда, когда система способна адаптироваться к изменениям состояний её элементов.
2013-03-20 11:15:00 (читать в оригинале)

Самоорганизующиеся системы связи и их основные особенности
Введение
Наверное, вы не раз задумывались над поразительным отличием систем, которые существуют в природе, от систем, созданных человеком (например, современными системами связи). Первые - устойчивы к внешним воздействиям и склонны к росту и развитию. Для вторых – характерно резкое ухудшение их функционирования даже при незначительных нарушениях условий эксплуатации или при ошибках в управлении.
Само собой напрашивается вывод: нужно позаимствовать опыт организации систем, который накоплен природой, и использовать этот опыт в нашей деятельности. Но, для этого необходимо выяснить основные законы построения «природных» систем, основные принципы их организации, а также механизмы возникновения и изменения порядка в этих системах. При этом основное внимание должно быть сосредоточено не на процессах управления обменом информацией(будем считать, что эти процессы нам хорошо известны), а на принципах построения, организации и развития таких систем.
Подобного рода идеи достаточно глубоко рассматривались ещё в первой половине прошлого столетия, но, в силу относительно скромных технических возможностей того времени, широкого практического применения в системах связи не нашли. В настоящее же время активно разрабатываются системы, в которых многие задачи (в основном, связанные с маршрутизацией) решаются автоматически. Такие системы, основаны на представлении всех возможных структур системы как её состояний, возникающих в результате многовариантного и неоднозначного воздействия на эту систему «извне».
Но более интересны (и, по-видимому, ещё более перспективны) те системы, которые способны не только к адаптации к случайно сложившимся ситуациям, но и к образованию новых структур, которые более сложны, чем исходные. Такая способность в какой-то степени соответствует естественному механизму природного движения: от элементарного и примитивного — к более сложному и более совершенному.
Основным особенностям таких систем (применительно к вопросам организации связи) и посвящена данная статья. В этом статье рассмотрены:
● основные признаки организации и самоорганизации;
● один из возможных критериев оценки качества организации;
● методика оценки системы по данному критерию (на конкретных примерах);
● возможный вариант структуры системы управления системой связи.
Если вас заинтересует данная проблема, то кое-какая информация может быть получена из Интернета. Ключевые слова: открытая система, кибернетика, синергетика,энтропия.
Основные свойства организованных и самоорганизующихся систем
Известно, что система может считаться организованной, если она обладает следующими свойствами:
Система должна быть открытой, то есть система должна реагировать на какие либо внешние воздействия.
Организация может иметь место лишь в системах достаточного уровня сложности,поскольку недостаточно сложные системы не способны ни к спонтанной адаптации, ни, тем более, к эволюции.
Фундаментальный принцип организации –возможность возникновения нового порядка через флуктуациисостояний элементов системы.
Такие флуктуации (случайные отклонения) могут подавляться за счёт отрицательных обратных связей, обеспечивающих сохранение прежнего состояния системы (например, с помощью механизмов адаптации к случайным сбоям её элементов).
Но в более сложных открытых системах, могут использоваться алгоритмы коллективного поведения элементов и подсистем, которые, через кратковременное «хаотическое» состояние, приводят, либо к разрушению прежней структуры, либо к возникновению нового порядка. Яркий пример – «взрывной» характер потоков служебной информации при адаптации к изменениям состояний линий сети связи, которые могут возникнуть при использовании динамической маршрутизации.
Открытая система должна быть достаточно далека от «точки равновесия»(тупиковой ситуации). В точке равновесия (тупике) сколь угодно сложная система не способна к какой-либо организации. В положении, близком к «равновесию» и без достаточного притока воздействий на систему извне, любая система будет неуклонно приближаться к «гибели», поскольку организованная система не всегда способна возвращаться в то состояние, в котором она когда-то была.
Самоорганизующиеся системыдолжны обладать всеми перечисленными свойствами, и, кроме того, должны быть способны адаптироваться, как к необратимым разрушениям старых, так и к возникновению новых структур.
При этом, для того, чтобы предотвратить (или хотя бы отсрочить) «гибель» системы, самоорганизующаяся система должна иметь «внешнюю поддержку». Действительно, если изменение состояния системы обусловлено только воздействием суммы случайных факторов (например, спонтанными изменениями условий радиослышимости в системах связи), то «время жизни» такой системы будет ограничено и такая система не способна эффективно противостоять необратимым воздействиям внешней среды. Например, система связи может быть живучей только в том случае, если в ней будут присутствовать механизмы позитивного воздействия на эту систему, которые обеспечивают:
- ремонт (или замену) поврежденных узлов и линий;
- укрепление структуры системы путем ввода в её состав новых элементов;
- организацию маневров имеющимися ресурсами (частотами, каналами и т.д.).
Это свойство имеет решающее значение – только при получении ресурсов «извне» (и наличии механизмов «усвоения» этих ресурсов) система будет способна к эволюции. При недостатке же таких ресурсов, система будет постепенно деградировать.
Так же необходимо отметить, что очень важным является критерий качества организации системы.
Так же необходимо отметить, что очень важным является критерий качества организации системы.

Реализация модели канала
При построении алгоритма имитации работы всех каналов сети, сеть рассматривается как совокупность параллельно протекающих процессов. Каждый процесс есть некоторая последовательность событий, приводящих к изменению состояний синхронных автоматов, описывающих поведение элементов сети, причём, под событием понимается любое изменение сигналов на входах этих автоматов.
В общем случае, эти процессы не должны считаться независимыми, а а должны взаимодействовать между собой.
Принципы взаимодействия процессов могут быть проиллюстрированы следующим примером. Представим себе фрагмент сети, включающий в себя Nабонентов, работающий на одной и той же частоте. Такой фрагмент может рассматриваться как система массового обслуживания с одним прибором, который обслуживает некий поток требований от Nстанций. Если требование, придя в систему, застаёт прибор свободным, то оно занимает прибор и обслуживается в нём в течение некоторого промежутка времени, после чего покидает систему. В противном случае, требование поступает в очередь к прибору, где будет дожидаться завершения обслуживания всех ранее поступивших в систему требований. Причём эта очередь «виртуальна» - требования могут быть сосредоточены как в одном узле, так и распределены по разным узлам.
В такой системе, на начальных фазах обслуживания, «передатчик» каждого узла может находиться в одном из следующих состояний:
- ожидание очередного кадра;
- ожидание освобождения канала;
- запуск таймера, определяющего время начала передачи кадра (основной принцип канального протокола – «слушать», прежде чем «вещать»);
- ожидание завершения данного интервала;
- захват канала и передача кадра.
Переход «передатчика» из одного состояния в другое, осуществляется под воздействием комбинаций входных сигналов. Эти сигналы могут поступать, как извне - от модуля, имитирующего поведение «высшего» уровня, так и от других автоматов - автоматов того же уровня.
Например, (см. рисунок 1), переход автомата из состояния «ожидание кадра» в состояние «ожидание освобождения канала» осуществляется при появлении сигнала «требование передачи», а переход в следующее состояние – «запуск таймера отсрочки» - зависит от состояний аналогичных автоматов, претендующих на тот же канал.
Если какой либо другой аналогичный автомат находится в состоянии «захват канала», то рассматриваемый автомат будет получать сигнал «канал занят».
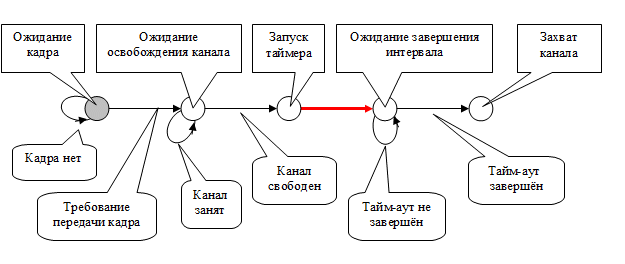
Рисунок 1
Из рассматриваемого примера видно, что в моделируемой сети могут сосуществовать параллельные «типовые» процессы, каждый из которых может находиться в своём уникальном состоянии. Но, при их имитации на одной ЭВМ, эти события необходимо рассматривать последовательно. Поэтому, совокупность параллельно протекающих процессов должна быть представлена в виде упорядоченной последовательности моментов наступления событий во времени.
При таких условиях, сканируя эту последовательность, и определяя, в каждый наступивший момент реакции автоматов на изменения входных сигналов, можно сымитировать любую ситуацию в системе. При этом, любая сложившаяся ситуация может быть представлена в виде вектора Z=║Zn║, каждый элемент которого - Zn, соответствует конкретному автомату - Mn, а значение этого элемента – состоянию данного автомата. Например, если некий автомат M1занял канал, (состояние St4), а автомат M2ожидает его освобождения (состояние St1), то фрагмент вектора Zбудет содержать информацию, которая показана на рисунке 2:
- Конечный автоматТекущее состояниеM1St4M2St1..
Рисунок 2
При наступлении особого состояния, (изменении входных сигналов), этот вектор модифицируется с помощью следующего алгоритма:
- поочерёдно рассматриваются состояния всех автоматов;
- при рассмотрении каждого состояния определяется соответствующая ему выходная комбинация - µ;
- на основании полученных µ отыскиваются входные комбинации для всех автоматов - λ;
- найденные входные комбинации фиксируются в памяти ЭВМ;
- с помощью таблиц переходов определяются новые состояния автоматов.
В принципе, такие операции («ревизии» состояний системы) можно производить на каждом такте имитации – любая ситуация может считаться особым состоянием.
Но такое решение нецелесообразно, поскольку потребует больших затрат машинного времени. Более целесообразно считать особыми состояниями только те ситуации, которые определяют моменты выхода автоматов из пассивных состояний - состояний ожидания.
В основном, моменты выхода из пассивных состояний определяются таймерами, поскольку именно они определяют моменты системного времени, соответствующие узловым точкам в имитируемых параллельных процессах.
Состояния этих таймеров – числа Tk, которые соответствуют моментам активизации тех или иных автоматов. Если таймер запущен, то это число должно каким-то образом уменьшаться, и в тот момент, когда оно станет равным нулю, заданный тайм-аут должен считаться завершённым.
Как в реальной системе, так и в имитационной модели, могут одновременно работать kтаймеров, причём каждый из них может завершить отсчёт в конкретный момент времени – Tk. Имея такие числа можно определить момент наступления ближайшего особого состояния системы, которое может быть определено с помощью проверки условия (1):
- TR = min Tk(1)k
Далее, после активизации соответствующих процессов, значения всех запущенных таймеров уменьшается на величину TR, позволяя тем самым определить момент наступления следующего особого состояния.
Следует отметить, что особые события могут порождаться не только таймерами, но и всеми другими автоматами. Причём эти автоматы могут находиться в пассивных состояниях, время выхода из которых – Ta, определить нельзя.
В таких случаях возможно следующее решение – если входной сигнал не меняет состояния автомата, то считать Ta= ∞. В противном же случае считать, что Ta= 0.
Для определения значения Taможно воспользоваться таблицей переходов, действуя следующим образом:
- выделить строку такой таблицы, которая соответствует текущему состоянию автомата;
- убедиться в том, что текущая комбинация входных сигналов соответствует «петле», то есть возвращает автомат в то же состояние, в котором он уже находиться;
- если это условие выполняется – то Ta : = ∞, в противном случае - Ta : = 0.
Например, в представленной на рисунке 3 таблице переходов, выделенные элементы соответствуют активным состояниям автомата, которые следует считать особыми событиями, а все остальные элементы – пассивным состояниям автомата.
- СостояниеСимволы входного алфавитаλ0λ1λ2λ3λ4λ5λ*St0St0St1St4St4---St1St2St1St4St4---St2------St3St3----St3--St4St0-St4St4---
Рисунок 3
Рассмотренный принцип имитации поведения сложных систем с дискретными событиями может являться основой для построения других аналогичных моделей. При этом программные модули, обеспечивающие имитацию квазипараллельных процессов в системе, могут оставаться неизменными – если потребуется исследовать поведение групповых каналов, основанных на использовании иных протоколов, то программное обеспечение может оставаться неизменным, и только модели поведения «передатчиков» и «приёмников» могут быть представлены в виде таблиц иного содержания.
В то же время, данный принцип может являться основой для обеспечения наглядной интерпретации поведения системы. Но это возможно лишь только в том случае, если основными мотивами расчленения модели на операторы и блоки (конечные автоматы) будут являться не только «вычислительные удобства» для программистов, но и категории, понятия и образы, которые понятны и привычны для большинства специалистов, работающих в данной области.
2013-03-11 11:04:00 (читать в оригинале)

Имитационная модель канала коллективного доступа
В предыдущей статье мы оценивали вероятность успешного захвата канала в конкурентном окне.
В предыдущей статье мы оценивали вероятность успешного захвата канала в конкурентном окне.
Имитация процессов передачи и приёма кадра
1.1. В упрощенном виде, процесс передачи кадра по радиолучу (Xi, Xj) может быть представлен, как поведение композиции конечных автоматов, которая изображена на рисунке 1:
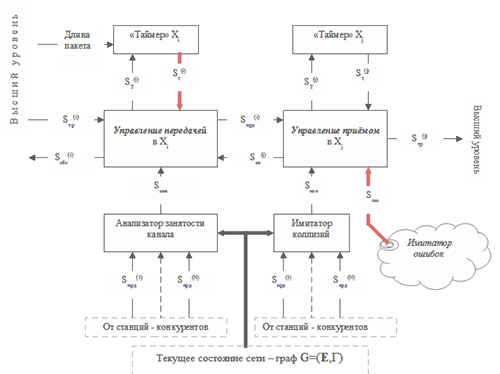
Рисунок 1
1.2. Изображённый на рисунке 1 «Таймер» Xiпредназначен для определения моментов времени, соответствующих:
1) времени отсрочки начала передачи очередного пакета (кадра);
2) времени завершения передачи;
3) времени ожидания «квитанции».
При этом, поведение этого «таймера» может быть, как детерминировано (при определении момента времени, соответствующего завершению передачи пакета), так и псевдослучайным (при вычислении времени отсрочки начала передачи).
1.3. «Таймер» Xj– определяет момент начала и завершения передачи квитанции, причём поведение этого таймера всегда детерминировано. Следует отметить, что, как «Таймер» Xi, так и «Таймер» Xi, ведут отсчёт интервалов времени в особых условных единицах – «тиках».
Предположительно, один «тик» имитирует интервал времени, соответствующий длительности одного «слота».
1.4. Автомат, который имитирует процесс управления передачей кадра по радиолучу (Xi, Xj) фактически выполняет функции «диспетчера», взаимодействующим со своим «окружением» с помощью следующих сигналов:
1) сигналов Sтр(i) и Sобс(i), обеспечивающих взаимодействие с протоколом «высшего» уровня, который «поставляет» кадры для передачи, причём:
- сигнал Sтр(i) соответствует поступлению очередного требования на передачу кадра;
- сигнал Sобс(i), который соответствует запросу очередного требования на обслуживание, когда предыдущая заявка на обслуживание уже выполнена.
2) сигналов ST(i) и S(i), первый из которых определяет тип интервала времени, а именно:
- времени отсрочки передачи пакета;
- времени завершения передачи пакета;
- времени ожидания квитанции,
а второй – S(i) – завершению отсчёта заданного интервала.
3) сигналов Sпрд(i) и Sкв(j), обеспечивающих имитацию взаимодействия с «приёмной стороной» (автоматом «Управление приёмом в Xj»). При этом сигнал Sпрд(i)= 1 оповещает все «станции» Xjо том, что передатчик Xiнаходится в состоянии передачи.
4) и, наконец, сигнала Sзан, запрещающего выход в эфир, формируемого «анализатором занятости канала». Данный анализатор представляет собой тривиальный автомат, реализующий булеву функцию (1):
- Sзан = A1i Sпрд(1) v A2i Sпрд(2) v . . . v ANi Sпрд(N)(1)
где
- Aki (k=1, 2, . . . , N) – элементы матрицы смежности A=║Aij║, описывающей граф G=(E,Г), соответствующий текущему состоянию сети;
- Sпрд(k)(k=1, 2, . . . , N) – значения сигналов, соответствующих состояниям конкурирующих станций: если конкурент Xkведёт передачу, то Sпрд(k) =1.
- N– число узлов в сети.
Следует отметить, что функция (1) может быть использована только в том случае, если все узлы сети работают на одной и той же частоте. Если же это условие не выполняется, то функция (1) должна быть дополнена действием (2):
- Sпрд(k) : = 0, если Xiwi, Xjwi, но Xkwi(2)
1.5. Хотя функции (1) и (2) и тривиальны, но, по-видимому, требуют пояснений. Для этого рассмотрим следующий пример. Пусть условия радиослышимости описываются графом, который изображён на рисунке 2:

Рисунок 2
Такому графу будет соответствовать матрица A=║Aij║, которая представлена на рисунке 3:
- XiXjXbXcXdXi01111Xj10011Xb10010Xc11101Xd01010
Рисунок 3
Теперь предположим, что на частоту wiпретендуют передатчик Xiи его конкуренты – станции Xbи Xd. Сравнивая пары значений AkiSпрд(k), получим картину, представленную на рисунке 4:
- AkiSпрд(k)Xi0&1= 0Xj1&0= 0Xb1&1= 1Xc1&0= 0Xd0&1= 0
Рисунок 4
Это означает, что станция Xiспособна уступить канал станции Xb, но никогда не обнаружит каких-либо признаков активности со стороны станции Xd. Но, это - особенность IEEE802.11 ….
1.6. Поведение автомата «Управление передачей» может быть описано диаграммой состояний, представленной на рисунке 5:

Рисунок 5
Данный автомат может находиться в одном из восьми состояний:
- St0 – исходное состояние - ожидание заявки на передачу кадра;
- St1 – ожидание освобождения канала;
- St2 – запуск таймера, обеспечивающего отсчёт времени отсрочки начала передачи пакета, а также момента времени завершения его передачи;
- St3 – ожидание собственного «слота»;
- St4 – передача пакета в эфир;
- St5 – запуск таймера ожидания квитанции;
- St6 – ожидание квитанции;
- St7 – оповещение о факте неудачной попытке передачи кадра.
Переходы данного автомата из одного состояния в другое осуществляются под воздействием символов входного алфавита - i, то есть под воздействием конкретных комбинаций входных сигналов. Эти комбинации приведены в таблице 1:
Таблица 1
- Символ входного алфавитаЗначения входных сигналовSтр(i)S(i)Sкв(i)Sзан(i)λ00xxx
Тэги: 802.11, wi-fi, имитационный, маршрутизация, моделирование, связь, сеть, телекоммуникация
Постоянная ссылка
2013-03-04 10:07:00 (читать в оригинале)

Вероятность успешного захвата канала в конкурентном окнеНапомним, ранее мы попытались оценить возможные потери при возникновении коллизий в канале коллективного доступа.В IEEE802.11 временной интервал, выделенный на захват канала какой-либо станцией, ограничен и разделён на более короткие интервалы – слоты, причём число таких слотов ограничено. При этом порядковый номер слота определяет время отсрочки процесса передачи пакета, привязанное к некоему событию, например, освобождению канала.Каждая станция выбирает «свой» слот случайным образом и выходит в эфир только в том случае, если выполняются следующие условия:- канал свободен;
- время отсрочки исчерпано.
Кроме того, будем считать, что захват одного и того же слота двумя и более станциями неизбежно приведёт к коллизиям.Общее число ситуаций, которые могут возникнуть при случайном «розыгрыше» слотов, будет равняться числу размещений с повторением из kпо S, и определяться выражением (1):- AkS = Sk+1(1)
где- S – общее число слотов;
- k+1 – общее число станций в «клике», включая рассматриваемую станцию «А».
Очевидно, что далеко не любая из этих ситуаций может привести к успешной передаче пакета. Например (см. рисунок 1), станция «А» может захватить и успешно использовать 1-й слот только тогда, когда её «конкуренты» будут претендовать только на захват последующих слотов.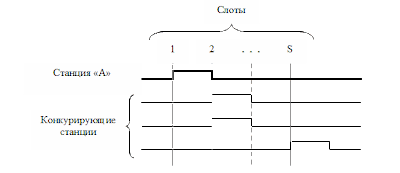 Рисунок 1Число таких ситуаций зависит от числа слотов - Sи числа «конкурентов» - k, и определяется выражением (2):
Рисунок 1Число таких ситуаций зависит от числа слотов - Sи числа «конкурентов» - k, и определяется выражением (2):- (S-1) k(2)
а вероятность захвата 1-го слота – выражением (3):P1 = (S-1) k / Sk+1
(3)
Станция «А» может успешно использовать и 2-й слот, но только в том случае, если ни одна из конкурирующих станций не будет претендовать ни на 1-й, ни на 2-й слоты.Соответствующий пример приведён на рисунке 2: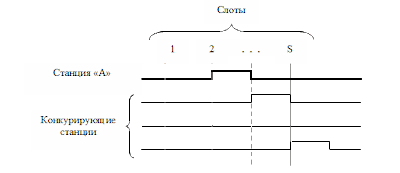 Рисунок 2Вероятность подобной ситуации будет определяться выражением (4):
Рисунок 2Вероятность подобной ситуации будет определяться выражением (4):- P2 = (S-2) k / Sk+1(4)
Аналогичным образом может быть определена вероятность успешного использования третьего слота – см. выражение (5):- P2 = (S-3) k / Sk+1(5)
В общем же случае, суммарная вероятность «победы» в конкурентной борьбе, нацеленной на захват канала, будет равняться величине Pзхв, которая может быть определена по формуле (6):- S-1Pзхв = P1 + P2 + ... + PS-1 = (S-i) k / Sk+1(6)i=1
Следует отметить, что формула (6) справедлива только при k>0. Очевидно, что, при k>0, последний слот не может быть захвачен и успешно использован двумя и более абонентами. Но если k=0, то последний, S-тый слот может быть также успешно использован, следовательно, величина Pзхвбудет равна единице.3.2.5. Графики функции (6) при различных значениях величины Sпредставлены на рисунке 3: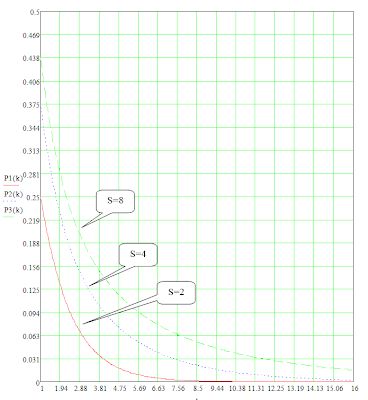 Рисунок 3Рассматривая приведённые графики можно прийти к следующему выводу: даже при небольшом числе конкурирующих станций, вероятность успешной попытки захвата канала очень мала. Причём увеличение числа слотов повышает эту вероятность, но незначительно, а при большом числе конкурентов стремится к нулю.Пренебрегать этим обстоятельством нельзя, и очевидно, что имитация механизмов противодействия коллизиям (как на канальном, так и прикладном уровнях) должна рассматриваться как неотъемлемая часть разрабатываемой модели.Но при этом необходимо ответить на следующий вопрос, - какой способ имитации этих процессов наиболее целесообразен?Рассмотренные в данном разделе методики обладают рядом положительных качеств. Задачи решены «в общем виде» и не привязаны к конкретным числовым значениям параметров потока и системы обслуживания, что позволяет делать полезные общие заключения.Но, к сожалению, эти методики позволяют находить общие решения для задач, сводящихся к элементарным ситуациям – то есть в случаях, когда поток заявок невелик и на один и тот же канал будут претендовать одна-две станции.В принципе, такое допущение возможно и может считаться достаточно корректным. Например, при имитации движения пользовательского трафика можно считать, что нагрузка на любой канал не должна превышать 80% его производительности, поскольку в противном случае очереди в узлах будут стремительно расти. Для того, чтобы убедиться в этом, достаточно рассмотреть график, который приведён на рисунке 4:
Рисунок 3Рассматривая приведённые графики можно прийти к следующему выводу: даже при небольшом числе конкурирующих станций, вероятность успешной попытки захвата канала очень мала. Причём увеличение числа слотов повышает эту вероятность, но незначительно, а при большом числе конкурентов стремится к нулю.Пренебрегать этим обстоятельством нельзя, и очевидно, что имитация механизмов противодействия коллизиям (как на канальном, так и прикладном уровнях) должна рассматриваться как неотъемлемая часть разрабатываемой модели.Но при этом необходимо ответить на следующий вопрос, - какой способ имитации этих процессов наиболее целесообразен?Рассмотренные в данном разделе методики обладают рядом положительных качеств. Задачи решены «в общем виде» и не привязаны к конкретным числовым значениям параметров потока и системы обслуживания, что позволяет делать полезные общие заключения.Но, к сожалению, эти методики позволяют находить общие решения для задач, сводящихся к элементарным ситуациям – то есть в случаях, когда поток заявок невелик и на один и тот же канал будут претендовать одна-две станции.В принципе, такое допущение возможно и может считаться достаточно корректным. Например, при имитации движения пользовательского трафика можно считать, что нагрузка на любой канал не должна превышать 80% его производительности, поскольку в противном случае очереди в узлах будут стремительно расти. Для того, чтобы убедиться в этом, достаточно рассмотреть график, который приведён на рисунке 4: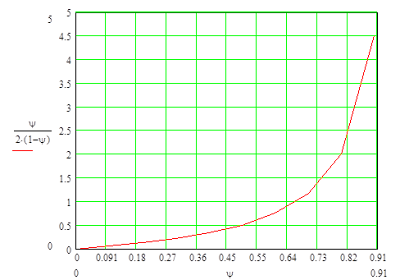 Рисунок 4Этот график показывает зависимость времени пребывания пакета в очереди от нагрузки на канал - Ψ=λ/μ, где λ – интенсивность потока заявок, а μ – производительность канала. (при построении графика предполагалось, что поток заявок – Пуассоновский, а время обслуживания – постоянное). Время ожидания показано в условных единицах: одна условная единица – время обслуживания одного пакета.Тогда, рассматривая этот график можно прийти к следующему заключению: при Ψ=0.8 средняя величина очереди на канал равна двум. И можно допустить, что ситуации, при которых на один и тот же канал будут претендовать более 2-х станций, не представляют интереса, поскольку строить сети с «бесконечными» очередями не имеет смысла.
Рисунок 4Этот график показывает зависимость времени пребывания пакета в очереди от нагрузки на канал - Ψ=λ/μ, где λ – интенсивность потока заявок, а μ – производительность канала. (при построении графика предполагалось, что поток заявок – Пуассоновский, а время обслуживания – постоянное). Время ожидания показано в условных единицах: одна условная единица – время обслуживания одного пакета.Тогда, рассматривая этот график можно прийти к следующему заключению: при Ψ=0.8 средняя величина очереди на канал равна двум. И можно допустить, что ситуации, при которых на один и тот же канал будут претендовать более 2-х станций, не представляют интереса, поскольку строить сети с «бесконечными» очередями не имеет смысла.
Далее мы рассмотрим имитационную модель канала коллективного доступа.
Тэги: 802.11, wi-fi, имитационный, маршрутизация, моделирование, связь, сеть, телекоммуникация
Постоянная ссылка


 Категория «Новости»Взлеты Топ 5
Категория «Новости»Взлеты Топ 5
+903
934
Блог о подарках и праздниках
+883
955
Kitten
+876
942
And_So_On
+846
1007
Уголок народного трейдера
+814
958
ank
Падения Топ 5
-1
4
Equillibrium
-1
255
Главная
-2
15
Elephant_Talk
-6
5
lqp
-6
771
Сибдепо / Блоги
 Популярные за сутки
Популярные за сутки
Загрузка... BlogRider.ru не имеет отношения к публикуемым в записях блогов материалам. Все записи
BlogRider.ru не имеет отношения к публикуемым в записях блогов материалам. Все записи
взяты из открытых общедоступных источников и являются собственностью их авторов.
