| Сегодня 25 ноября, понедельник |
      |
  
|
  
Какой рейтинг вас больше интересует?
|
Главная /
Каталог блоговCтраница блогера Что интересного происходит в науке/Записи в блоге |
 |
Что интересного происходит в науке
Голосов: 1 Адрес блога: http://igorivanov.blogspot.com/ Добавлен: 2008-05-17 13:57:21 блограйдером Lurk |
Орбитальный угловой момент фотона — 2
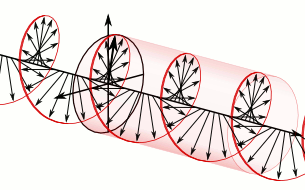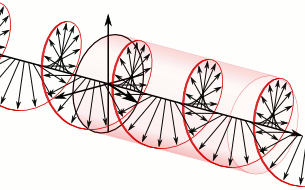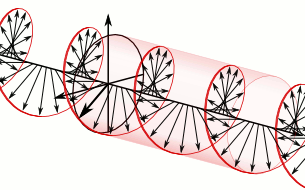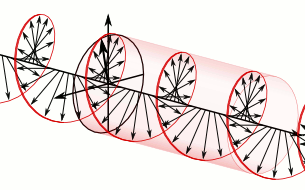
2011-05-06 01:49:00 (читать в оригинале)В продолжение темы про фотоны с орбитальным угловым моментом (ОУМ) — вот чуть более технический пост про то, как орбитальный угловой момент уживается с поляризацией.знаменитая такая картинка, на которой световая волна изображена этакой крутящейся спиралью:
Она похожа на ту, что я приводил в прошлом посте.
Но надо понимать, что на верхней картинке изображено вовсе не распределение электрического поля в реальном пространстве, а лишь условно показан вектор этого поля вдоль оси движения волны. Эта картинка не меняется при смещении в поперечном направлении, поскольку в плоской волне никакой зависимости полей от поперечных координат нет. Т.е. реально такая волна (если бы мы рисовали именно фазу волны, а не вектор электрического поля) бежит просто вперед, одна плоскость за другой.
А вот на картинке с закрученной волной (скалярной волной, т.е. волной не имеющей никакой поляризации) винтовая поверхность — это поверхность постоянной фазы в реальном пространстве. Такая волна действительно бежит вперед, одновременно накручиваясь вокруг оси.
Разделение спина и ОУМ
На самом деле, во всей этой истории с фотонами, несущими орбитальный угловой момент, есть один сложный и глубокий вопрос — в какой степени можно вообще разделять полный угловой момент фотона на орбитальную и спиновую часть.
Спин (т.е. поляризация) и орбитальный момент — это две разновидности полного момента импульса. В квантовой механике эти две величины описываются своими операторами:
и 
, а оператор полного спина есть просто их сумма 
. В квантовой механике по построению понятно, что есть ОУМ и что есть спин, поэтому вопросов об их разделении не возникает.
В теории поля (даже не-квантовой) всё хитрее. Там мы вводим многокомпонентное поле и изучаем, как оно преобразуется при переходе к другой системе координат или системе отсчета. Из этого рассмотрения само вытекает понятие сохраняющего углового момента и понятие спина. Полный момент импульса J (а точнее, его плотность) для электромагнитного поля легко записывается через электрическое и магнитное поля:
. Эта величина калибровочно-инвариантна и потому наблюдаема.
Однако в квантовой теории разделить ее на два векторных оператора, орбитальный и спиновый, которые обладали бы правильными коммутационными свойствами и были бы еще калибровочно-инвариантными, не удается. Поэтому возникает впечатление, что разделение полного момента импульса на две части для этих частиц нефизично.
Разделение спина и ОУМ в сильных взаимодействиях
Эта проблема еще больше усугубляется в физике элементарных частиц, когда мы вместо электромагнитных взаимодействий рассматриваем сильные взаимодействия (вместо фотонов — глюоны, вместо электронов — кварки). Теория сильных взаимодействий неабелева и потому нелинейна; в ней отделить свойства кварков от свойств глюонов еще тяжелее. Поэтому тут вопрос о том, можно ли разумным образом ввести орбитальный угловой момент кварков и глюонов встает в полный рост.
И это не праздный интерес. Дело в том, что уже давно известно, что спин быстро летящего поляризованного протона вовсе не складывается из одних лишь спинов кварков (это так называемая «загадка спина протона», краткий обзор нынешней ситуации см. в arXiv:0905.4619). На самом деле поляризация кварков дает совсем небольшой вклад, и значит, почти весь спин протона берется откуда-то еще. На наивном языке обычно приговаривают, что есть мол еще спин глюонов, а также орбитальный момент кварков и глюонов — и всё это должно вместе давать полный спин протона. Сейчас ведутся даже эксперименты, которые пытаются узнать, какой вклад вносят эти компоненты момента импульса в полный спин протона, а тут оказывается, теоретики спорят о том, как вообще определять эти вещи.
Над этой проблемой люди бьются вот уже десяток лет. Почувствуйте ситуацию: тут сложности не в том, как с помощью теории описать экспериментальные явления, а в том, как вообще правильно обращаться с теорией. Желающим посмотреть, что там за баталии, рекомендую недавнюю статью Эллиота Лидера arXiv:1101.5956; там есть сначала подробное обсуждение электродинамики, а затем сильных взаимодействий, и ссылки на разные предыдущие работы.
Так разделяются или нет?
Вернемся снова к фотонам. Что сейчас известно точно?
Во-первых, под разделением спина и ОУМ можно подразумевать разные вещи. Это может быть сильное утверждение о разделении операторов как векторов, может быть более слабое утверждение о разделении только z-компонент операторов (т.е. спиральностей), а может быть и еще более слабое утверждение об осмысленном разделении средних значений этих операторов по тем или иным состояниям фотонов.
Во-вторых, если говорить про самое слабое утверждение, то в параксиальном приближении (т.е. световая волна очень плавно меняется в поперечной плоскости) оно работает. Доказывается это несложно. Мы пишем вектор-потенциал с закрученным профилем (с числом закрутки m) и считаем, что у него есть только одна компонента (например, по оси x), что отвечает линейной поляризации. Считаем плотность полного момента импульса (а он определен однозначно), делим его на плотность потока и получаем m/ω. На квантовом языке это означает, что каждый фотон несет m квантов полного углового момента.
Теперь запишем двухкомпонентный вектор-потенциал, причем его комплексные x и y компоненты сдвинуты по фазе на π/2 — это как раз отвечает круговой поляризации. Повторяем расчет и получаем (m+1)/ω для положительной спиральности и (m−1)/ω — для отрицательной. Т.е. спиновой и орбитальный вклад в средние значения момента импульса мило уживаются друг с другом.
А что будет, если выйти за пределы параксиального приближения? Если повторить те же расчеты, то окажется, что спин и ОУМ так просто не суммируются. Однако на эту ситуацию можно посмотреть еще и вот так: в непараксиальном закрученном свете наводится спин-орбитальное взаимодействие (и это в линейной волне!), которое и мешает этому разделению. Такую точку зрения предлагает Константин Блиох в статье arXiv:1006.3876 (и вот еще появившаяся на днях статья arXiv:1105.0331, где он то же описание разрабатывает для релятивистских закрученных электронов).
На всякий случай скажу, что сомнений в том, можно ли экспериментально получать световые пучки, комбинирующие орбитальную закрученность с поляризацией, не возникает — конечно, можно. Вопрос только в том, как правильно такие состояния описывать.
Экзотические поляризационные состояния
Напоследок, есть очень наглядное объяснение, почему непараксиальный случай вообще намного сложнее параксиального, когда дело касается поляризации.
В строгой плоской волне электрическое и магнитное поле лежат в плоскости, перпендикулярной направлению движения волны. Для не-плоской волны такой единой плоскости нет. В результате в какой-то выбранной точке вектор электрического поля может иметь все три компоненты. Конечно, локально этот вектор по-прежнему лежит в плоскости, ортогональной локальному направлению движения волны, но проблема в том, что эти плоскости разные для разных точек пространства.
Такая ситуация называется трехмерный свет. Описание такого поля поляризаций, которое меняется от точки к точке — отдельная интересная тема в оптике. Там есть разные поляризационные сингулярности и нетривиальные топологические штуки. Я как-то рассказывал про них в своем блоге и в новости Поляризация света может закручиваться наподобие ленты Мёбиуса.
В параксиальном приближении ситуация резко упрощается. Мы пренебрегаем z-компонентами полей, и фактически считаем, что все они лежат в единой плоскости. Это конечно резко упрощает описание, но при этом мы теряем некоторые богатства общего трехмерного света. Тем не менее, даже в этой упрощенной ситуации существуют необычные поляризационные состояния света — например, радиальная поляризация, показанная на рисунке выше.
А вот на картинке с закрученной волной (скалярной волной, т.е. волной не имеющей никакой поляризации) винтовая поверхность — это поверхность постоянной фазы в реальном пространстве. Такая волна действительно бежит вперед, одновременно накручиваясь вокруг оси.
Разделение спина и ОУМ
На самом деле, во всей этой истории с фотонами, несущими орбитальный угловой момент, есть один сложный и глубокий вопрос — в какой степени можно вообще разделять полный угловой момент фотона на орбитальную и спиновую часть.
Спин (т.е. поляризация) и орбитальный момент — это две разновидности полного момента импульса. В квантовой механике эти две величины описываются своими операторами:
В теории поля (даже не-квантовой) всё хитрее. Там мы вводим многокомпонентное поле и изучаем, как оно преобразуется при переходе к другой системе координат или системе отсчета. Из этого рассмотрения само вытекает понятие сохраняющего углового момента и понятие спина. Полный момент импульса J (а точнее, его плотность) для электромагнитного поля легко записывается через электрическое и магнитное поля:
Однако в квантовой теории разделить ее на два векторных оператора, орбитальный и спиновый, которые обладали бы правильными коммутационными свойствами и были бы еще калибровочно-инвариантными, не удается. Поэтому возникает впечатление, что разделение полного момента импульса на две части для этих частиц нефизично.
Разделение спина и ОУМ в сильных взаимодействиях
Эта проблема еще больше усугубляется в физике элементарных частиц, когда мы вместо электромагнитных взаимодействий рассматриваем сильные взаимодействия (вместо фотонов — глюоны, вместо электронов — кварки). Теория сильных взаимодействий неабелева и потому нелинейна; в ней отделить свойства кварков от свойств глюонов еще тяжелее. Поэтому тут вопрос о том, можно ли разумным образом ввести орбитальный угловой момент кварков и глюонов встает в полный рост.
 |
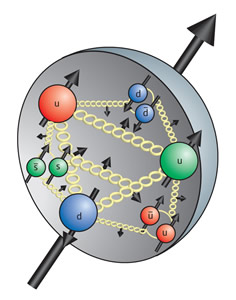| Из чего складывается спин быстро движущегося протона? Кто главнее: спин кварков, спин глюонов, их орбитальный угловой момент, или же это разделение вообще не очень осмысленно? |
И это не праздный интерес. Дело в том, что уже давно известно, что спин быстро летящего поляризованного протона вовсе не складывается из одних лишь спинов кварков (это так называемая «загадка спина протона», краткий обзор нынешней ситуации см. в arXiv:0905.4619). На самом деле поляризация кварков дает совсем небольшой вклад, и значит, почти весь спин протона берется откуда-то еще. На наивном языке обычно приговаривают, что есть мол еще спин глюонов, а также орбитальный момент кварков и глюонов — и всё это должно вместе давать полный спин протона. Сейчас ведутся даже эксперименты, которые пытаются узнать, какой вклад вносят эти компоненты момента импульса в полный спин протона, а тут оказывается, теоретики спорят о том, как вообще определять эти вещи.
Над этой проблемой люди бьются вот уже десяток лет. Почувствуйте ситуацию: тут сложности не в том, как с помощью теории описать экспериментальные явления, а в том, как вообще правильно обращаться с теорией. Желающим посмотреть, что там за баталии, рекомендую недавнюю статью Эллиота Лидера arXiv:1101.5956; там есть сначала подробное обсуждение электродинамики, а затем сильных взаимодействий, и ссылки на разные предыдущие работы.
Так разделяются или нет?
Вернемся снова к фотонам. Что сейчас известно точно?
Во-первых, под разделением спина и ОУМ можно подразумевать разные вещи. Это может быть сильное утверждение о разделении операторов как векторов, может быть более слабое утверждение о разделении только z-компонент операторов (т.е. спиральностей), а может быть и еще более слабое утверждение об осмысленном разделении средних значений этих операторов по тем или иным состояниям фотонов.
Во-вторых, если говорить про самое слабое утверждение, то в параксиальном приближении (т.е. световая волна очень плавно меняется в поперечной плоскости) оно работает. Доказывается это несложно. Мы пишем вектор-потенциал с закрученным профилем (с числом закрутки m) и считаем, что у него есть только одна компонента (например, по оси x), что отвечает линейной поляризации. Считаем плотность полного момента импульса (а он определен однозначно), делим его на плотность потока и получаем m/ω. На квантовом языке это означает, что каждый фотон несет m квантов полного углового момента.
Теперь запишем двухкомпонентный вектор-потенциал, причем его комплексные x и y компоненты сдвинуты по фазе на π/2 — это как раз отвечает круговой поляризации. Повторяем расчет и получаем (m+1)/ω для положительной спиральности и (m−1)/ω — для отрицательной. Т.е. спиновой и орбитальный вклад в средние значения момента импульса мило уживаются друг с другом.
А что будет, если выйти за пределы параксиального приближения? Если повторить те же расчеты, то окажется, что спин и ОУМ так просто не суммируются. Однако на эту ситуацию можно посмотреть еще и вот так: в непараксиальном закрученном свете наводится спин-орбитальное взаимодействие (и это в линейной волне!), которое и мешает этому разделению. Такую точку зрения предлагает Константин Блиох в статье arXiv:1006.3876 (и вот еще появившаяся на днях статья arXiv:1105.0331, где он то же описание разрабатывает для релятивистских закрученных электронов).
На всякий случай скажу, что сомнений в том, можно ли экспериментально получать световые пучки, комбинирующие орбитальную закрученность с поляризацией, не возникает — конечно, можно. Вопрос только в том, как правильно такие состояния описывать.
Экзотические поляризационные состояния
Напоследок, есть очень наглядное объяснение, почему непараксиальный случай вообще намного сложнее параксиального, когда дело касается поляризации.
В строгой плоской волне электрическое и магнитное поле лежат в плоскости, перпендикулярной направлению движения волны. Для не-плоской волны такой единой плоскости нет. В результате в какой-то выбранной точке вектор электрического поля может иметь все три компоненты. Конечно, локально этот вектор по-прежнему лежит в плоскости, ортогональной локальному направлению движения волны, но проблема в том, что эти плоскости разные для разных точек пространства.
Такая ситуация называется трехмерный свет. Описание такого поля поляризаций, которое меняется от точки к точке — отдельная интересная тема в оптике. Там есть разные поляризационные сингулярности и нетривиальные топологические штуки. Я как-то рассказывал про них в своем блоге и в новости Поляризация света может закручиваться наподобие ленты Мёбиуса.
 |
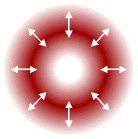| Радиально поляризованный свет:вектор электрического поля направлен вдоль радиус-вектора. |
В параксиальном приближении ситуация резко упрощается. Мы пренебрегаем z-компонентами полей, и фактически считаем, что все они лежат в единой плоскости. Это конечно резко упрощает описание, но при этом мы теряем некоторые богатства общего трехмерного света. Тем не менее, даже в этой упрощенной ситуации существуют необычные поляризационные состояния света — например, радиальная поляризация, показанная на рисунке выше.
AMS-02: детектор элементарных частиц в космосе
2011-04-29 03:28:00 (читать в оригинале)Вот церновский пресс-релиз, вот тут будет вестись онлайн-трансляция запуска начиная с 21:30 по средне-европейскому времени, твиттер ЦЕРНа тоже будет передавать сводки. Запуск и всю последующую работу можно отслеживать на сайте эксперимента. А я пока вкратце расскажу про аппарат и научные задачи.ATLAS, он не сравнится, но для запуска в космос (и установки на МКС) и этого немало.
Если подземные детекторы регистрируют частицы, родившиеся при рукотворном столкновении протонов и иных частиц, то AMS-02 будет регистрировать космические лучи — частицы очень больших энергий, прилетающие к нам из глубокого космоса, разогнанные на «природных ускорителях». Космические лучи, конечно, изучаются уже давно, почти век, но с ними до сих пор связано много загадок.
Самая главная задача нового детектора — со сверхвысокой точностью измерить состав космических лучей. Какова доля антивещества в космических лучях? Как она изменяется с энергией? Нет ли там в небольших количествах каких-то новых тяжелых стабильных частиц (частиц темной материи), которые не удается родить на коллайдерах, но которые смогла породить Вселенная? А может быть, какие-то тонкие особенности в энергетическом спектре обычных частиц укажут на то, что они получились при распаде неизвестных до сих пор сверхтяжелых частиц?
AMS-02 будет изучать эти вопросы, регистрируя пролет частиц космических лучей сквозь вещество детектора и измеряя их импульс, скорость, энерговыделение, заряд. «Окно» оптимальной чувствительности детектора по энергии частиц — от примерно 1 ГэВ до нескольких ТэВ. Это окно покрывает предсказания многих моделей, а также пересекается с окнами чувствительности детекторов на LHC. Но в отличие от Большого адронного коллайдера, тут в качестве ускорителя выступает сама вселенная, и это может иметь далеко идущие последствия.
 |
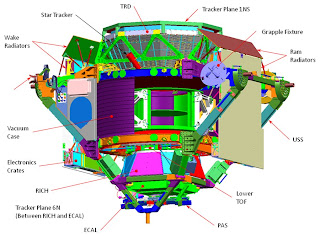| Субдетекторы и подсистемы AMS-02 (источник). |
Так же, как и классические наземные (точнее, подземные) детекторы, он содержит сразу несколько отдельных детектирующих систем, измеряющих разные характеристики частиц. Только в отличие от них, AMS-02 не вглядывается «вовнутрь», а «смотрит наружу»; он похож скорее на один сегмент передового современного детектора.
Кратко устройство описано на сайте эксперимента. Тут есть и трековые детекторы, восстанавливающие траекторию, черенковские детекторы, измеряющие скорость частиц, электромагнитные калориметры, измеряющие энергию частиц, и другие системы.
Строилось это всё 10 лет, стоимость — порядка 1,5 гигадолларов. В коллаборации AMS числятся 56 институтов из 16 стран.
Главное, чтоб сейчас эта штука удачно улетела. Завтра вечером будем следить за запуском!
Орбитальный угловой момент фотона
2011-04-24 16:28:00 (читать в оригинале)После недавнего поста Сергея Попова и моего (и не только) спора с ним про фотоны, приобретающие орбитальный угловой момент в окрестностях вращающихся черных дыр, я решил кое-что поподробнее написать про закрученный свет вообще.
Поверхность в виде штопора на этом рисунке — это поверхность постоянной фазы, т.е. те точки пространства, в которых волна находится в одинаковой фазе колебания. Стрелочки, перпендикулярные этой поверхности и идущие по винтовым линиям, показывают локальное направление движения волны. Для обычной плоской волны поверхности постоянной фазы — это просто плоскости, а перпендикулярные стрелочки везде были бы строго параллельны друг другу. А тут поверхность закручивается, и эти стрелочки как бы «обертывают» ось движения.
Именно это обертывающее движение и придает волне «в целом» некоторое вращение: волна летит вперед и вращается вокруг оси движения. Но получается это не из-за того, что волна крутится как твердое тело, а из-за коллективного эффекта наложения волн. Тем не менее это самое настоящее вращение в пространстве. Такая волна несет момент импульса, и если какое-то тело ее поглотит, то момент импульса передастся ему, и оно начнет вращаться.
Немножко формул
На рисунок можно взглянуть и чуть иначе. Представьте себе, что вы рассекаете эту волну плоскостью, перпендикулярной оси z (оси движения волны «в целом»). Тогда разные точки на этой плоскости будут отвечать разным фазам волны. Если на этой плоскости вы обходите вокруг центральной точки по кругу, фаза волны будет постоянно расти, и на полном обороте набег фаз составит 2π. В комплексных обозначениях волновая функция обладает угловой зависимостью exp(iφ), где φ — угол на этой плоскости. Закрутить волну можно и сильнее, организовав на полном обороте набег фаз кратный 2π. Зависимость от угла будет exp(imφ) с каким-то целым числом m.
В классической механике момент импульса точечной частицы определяется через ее положение и импульс:
В волновой механике можно тоже использовать эту формулу (только для плотности момента импульса), но только надо уточнить, чему равен импульс волны (это ключевой шаг!). Это можно сделать, например, на квантово-механическом языке:
Спин и орбитальный угловой момент
В квантовой механике момент импульса имеет две разных составляющих: орбитальный угловой момент и спин. Всё, о чем говорилось выше — это именно орбитальный угловой момент, т.е. механическая закрученность волнообразного объекта вокруг оси. Спин — это другая характеристика, которая не связана с механическим движением объекта.
При описании света и в калибровочных теориях вообще осмысленное разделение полного момента импульса волны на орбитальный угловой момент и спин — это отдельная длинная песня, я пока этого касаться не буду. Я просто хочу подчеркнуть, что ОУМ — это совсем не спин, он существует и у бесспиновых частиц (выше как раз такой случай и рассматривался).
Экспериментальные достижения
Я наверно напишу потом более технический пост про частицы с ОУМ, но пока что кратко опишу экспериментальную ситуацию.
Может показаться, что такие закрученные волны организовать очень трудно. На самом деле лазерные лучи, несущие орбитальный угловой момент, были реализованы еще в 1992 году. Такой закрученный свет можно получить, выделяя и складывая возбужденные поперечные моды из лазерного луча, а можно и просто пропустить обычный луч через фазовую пластинку или специальную голограмму. Сейчас такой «закрученный свет» уже рутинно используется в атомной физике, в физике поверхности, им также очень интересуются люди из квантовой теории информации.
Без труда можно получить и закрученные радиоволны. Я как-то писал про станцию HAARP на Аляске, которая облучает ионосферу и смотрит, что там происходит. Так вот, в том же посте есть картинки свечения ионосферы, облученной радиоволнами с ненулевым орбитальным угловым моментом.
Получать закрученные фотоны с энергией выше оптического диапазона трудно. Сейчас есть предложения, как это можно сделать в рентгене и даже в области высоких энергий (в ГэВ-ной области), но пока что это не реализовано. Зато уже получены электронные волны, несущие орбитальный угловой момент. Буквально несколько месяцев назад были получены электроны с энергией 300 кэВ и орбитальным числами m ~ 100.
Тот или не тот орбитальный угловой момент?
А теперь я вернусь к спору, который состоялся у Сергея Попова в ЖЖ. Комментируя недавнюю работу про то, как фотоны приобретают орбитальный угловой момент при пролете вблизи вращающихся черных дыр, он отдельно выделял, что это «не совсем тот» угловой момент, что есть у крутящихся предметов; похожий, но не тот.
Я хочу подчеркнуть еще раз — и надеюсь, благодаря предыдущему тексту это станет яснее — что это не какой-то новый особый вид углового момента, а именно тот самый, обычный, родной вращательный момент импульса, связанный с движением в пространстве. Единственная необычность в его описании связана с тем, что мы его пишем для волны, а не для частицы. Разница тут не в самом угловом моменте, а в том, про какой объект мы говорим — про волну или про частицу.
И кирпич, вращающийся вокруг своей оси, и электрон, сидящий в атоме, скажем, в P-волне, и вот эти закрученные состояния света — все они обладают обычным орбитальным угловым моментом. Этот орбитальный угловой момент описывается одной и той же формулой
Недавний результат Тэватрона
2011-04-22 21:16:00 (читать в оригинале)Написал-таки подробную новость про результат коллаборации CDF двухнедельной давности — а то меня уже раз пять спрашивали, что это такое было.
Вообще, если погружаться в такого типа анализ, мне становится как-то не по себе: мало того, что в процессе обработки самих данных огромную роль играет моделирование, так еще в какой-то момент данные начинают смешивать с численными псевдоданными и делать отсюда какие-то выводы. Я в своей собственной работе в такие дебри обычно не залезаю, но иногда при сравнении своих вычислений с данными приходится вникать в то, что именно и как именно находят экспериментаторы. И в отдельных случаях у меня, мягко говоря, возникают вопросы.
В общем, посмотрим, что из этого казуса выйдет. Лично мое мнение, что это артефакт.
Update: чтоб не вставать два раза, кратко написал по поводу разгорающейся шумихи насчет якобы обнаруженного хиггсовского бозона.
Дни науки в Челябинске
2011-04-14 00:07:00 (читать в оригинале)Я сейчас участвую в «Днях науки в Челябинске» — очередном мероприятии из серии «Дни науки», которые фонд «Династия» проводит несколько раз в год в разных городах России. Насколько я понимаю, сейчас у них самая насыщенная программа из всего того, что они делали — целая неделя лекций, встреч, открытых уроков, мастер-класов для учителей с утра до вечера в нескольких населенных пунктах Челябинской области.
У меня тут пять разных занятий (некоторые к тому же повторяются): три разных темы со школьниками («Физика быстропротекающих процессов в задачах», «Всё состоит из атомов — и неожиданные следствия из этого простого факта» и «Необычные волны»), урок для учителей и популярная лекция для широкой аудитории про Большой адронный коллайдер.
Первые впечатления: действительно есть и школьники, и учителя, очень заинтересованных наукой. Ребята на первом занятии приятно удивили — больше полкласса активно решало задачки. Это очень приятно после Европы, где студенты как правило задач боятся и впадают в ступор, когда незнакомый человек предлагает им чего-то решить. А вот учителя показались довольно пассивными: с ними у меня тоже было решение задач (других), но их раскачать не очень получилось. Похоже, для них это был больший стресс, чем для детей :).
Был некоторый контакт с журналистами, но опять же абсолютно упругий. Я интервью не даю, потому что, во-первых, я не могу что-то рассказывать человеку, которому это неинтересно, которому надо только «поставить материал», а во-вторых, как я уже раньше говорил, я считаю вредной ту роль этакого благородного посредника между широкой публикой и учеными, которые агрессивно навязывают СМИ и ученым, и публике.
В дополнение к этому получилась какая-то странная ситуация, когда на челябинском портале было вывешено объявление об онлайн-конференции с моим (и не только) участием и когда уже начали собирать вопросы, но я про нее был вообще не в курсе. Я от участия отказался, потому что я не общаюсь через СМИ. Поэтому если тут есть кто-то из Челябинска, то я хочу сказать: вопросы мне можно и так задавать онлайн, без всяких специальных конференций, хотя бы в комментах к этому посту. Либо их можно будет задать лично до и после моей лекции про LHC, которая состоится в понедельник 18 апреля в 16:00 в зале «Сигма» ЮрГУ.
Мне кажется, такое общение напрямую, без посредников и ограничений по времени куда эффективнее.
